Question
Question: $\lim_{n \to \infty} n^2 \int_{-1/n}^{1/n} (2010\sin x + 2012 \cos x) |x| dx$...
limn→∞n2∫−1/n1/n(2010sinx+2012cosx)∣x∣dx
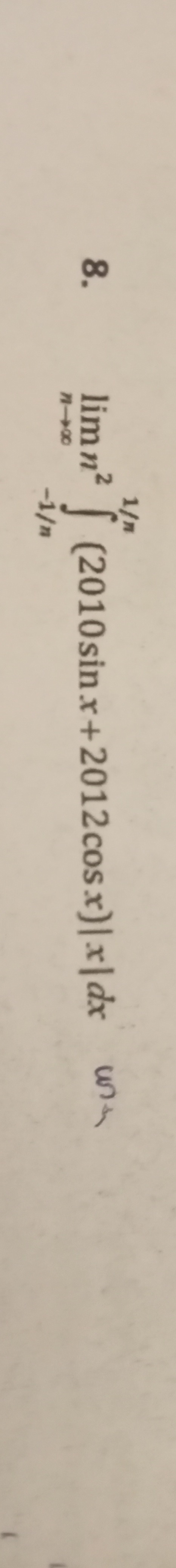
2012
Solution
Let the integral be denoted by In: In=∫−1/n1/n(2010sinx+2012cosx)∣x∣dx
We can split the integral based on the definition of ∣x∣: In=∫−1/n0(2010sinx+2012cosx)(−x)dx+∫01/n(2010sinx+2012cosx)(x)dx
In the first integral, let u=−x. Then du=−dx. When x=−1/n, u=1/n. When x=0, u=0. The first integral becomes: ∫1/n0(2010sin(−u)+2012cos(−u))(u)(−du) =∫1/n0(−2010sinu+2012cosu)(u)(−du) =∫01/n(−2010sinu+2012cosu)udu
Replacing the variable u with x: =∫01/n(−2010xsinx+2012xcosx)dx
Now, substitute this back into the expression for In: In=∫01/n(−2010xsinx+2012xcosx)dx+∫01/n(2010xsinx+2012xcosx)dx In=∫01/n[(−2010xsinx+2012xcosx)+(2010xsinx+2012xcosx)]dx In=∫01/n(4024xcosx)dx In=4024∫01/nxcosxdx
To evaluate the integral ∫xcosxdx, we use integration by parts (∫udv=uv−∫vdu): Let u=x and dv=cosxdx. Then du=dx and v=sinx. ∫xcosxdx=xsinx−∫sinxdx=xsinx−(−cosx)=xsinx+cosx.
Now, evaluate the definite integral: In=4024[xsinx+cosx]01/n In=4024[(n1sin(n1)+cos(n1))−(0sin(0)+cos(0))] In=4024(n1sin(n1)+cos(n1)−1)
We need to find the limit of n2In as n→∞: limn→∞n2In=limn→∞n2⋅4024(n1sin(n1)+cos(n1)−1) Let h=1/n. As n→∞, h→0. The expression becomes: 4024limh→0h21(hsinh+cosh−1) =4024limh→0h2hsinh+cosh−1
This is an indeterminate form of type 00. We can use Taylor series expansions for sinh and cosh around h=0: sinh=h−6h3+O(h5) cosh=1−2h2+24h4+O(h6)
Substitute these into the numerator: hsinh+cosh−1=h(h−6h3+...)+(1−2h2+24h4+...)−1 =h2−6h4+...+1−2h2+24h4+...−1 =(h2−2h2)+(−6h4+24h4)+... =2h2−243h4+... =2h2−8h4+...
Now, substitute this back into the limit: 4024limh→0h22h2−8h4+... =4024limh→0(21−8h2+...) =4024(21) =2012
Alternatively, using L'Hopital's Rule on limh→0h2hsinh+cosh−1: Applying L'Hopital's rule once: limh→0dhd(h2)dhd(hsinh+cosh−1)=limh→02hsinh+hcosh−sinh =limh→02hhcosh=limh→02cosh=21
The total limit is 4024×21=2012. The final answer is 2012.
