Question
Question: Let x,y,z be positive real numbers, then the least value of $\frac{x(1+y)+y(1+z)+z(1+x)}{\sqrt{xyz}}...
Let x,y,z be positive real numbers, then the least value of xyzx(1+y)+y(1+z)+z(1+x) is equal to-
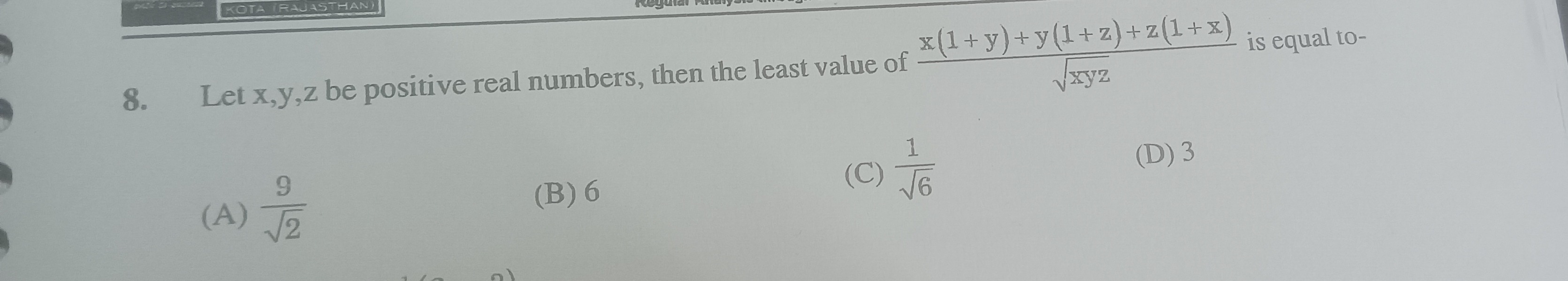
29
6
61
3
6
Solution
The given expression is E=xyzx(1+y)+y(1+z)+z(1+x).
First, expand the numerator: E=xyzx+xy+y+yz+z+zx
Rearrange the terms in the numerator: E=xyz(x+y+z)+(xy+yz+zx)
Now, we apply the AM-GM inequality to the terms in the numerator. For positive real numbers x,y,z:
- x+y+z≥33xyz
Equality holds when x=y=z.
- xy+yz+zx≥33(xy)(yz)(zx)
xy+yz+zx≥33x2y2z2
xy+yz+zx≥3(xyz)2/3
Equality holds when xy=yz=zx. Since x,y,z are positive, this implies x=y=z.
Substitute these inequalities into the expression for E: E≥(xyz)1/23(xyz)1/3+3(xyz)2/3
Now, simplify the powers of xyz: E≥3(xyz)1/2(xyz)1/3+3(xyz)1/2(xyz)2/3
E≥3(xyz)1/3−1/2+3(xyz)2/3−1/2
E≥3(xyz)2/6−3/6+3(xyz)4/6−3/6
E≥3(xyz)−1/6+3(xyz)1/6
Let t=(xyz)1/6. Since x,y,z are positive real numbers, t must be a positive real number. The inequality becomes:
E≥3t−1+3t
E≥3(t1+t)
Finally, apply the AM-GM inequality to t and t1: For any positive real number t, t+t1≥2t⋅t1
t+t1≥21
t+t1≥2
Equality holds when t=t1, which implies t2=1. Since t>0, we must have t=1.
Substitute this back into the expression for E: E≥3(2)
E≥6
To confirm that 6 is the least value, we need to show that equality can be achieved. All the AM-GM steps yield equality if:
- x=y=z
- t=1, which means (xyz)1/6=1, so xyz=1.
If x=y=z and xyz=1, then x⋅x⋅x=1, so x3=1. Since x is a positive real number, x=1. Therefore, when x=y=z=1, all the conditions for equality are met.
Let's calculate the value of E when x=y=z=1: E=1⋅1⋅11(1+1)+1(1+1)+1(1+1)
E=11(2)+1(2)+1(2)
E=12+2+2
E=6
Since the value 6 can be achieved, and we have shown E≥6, the least value of the expression is 6.
