Question
Question: Let $w$ be a complex number such that $w^5 = 1$ but $w \neq -1$. Then $(1 + w)^{-1}$ is equal to...
Let w be a complex number such that w5=1 but w=−1. Then (1+w)−1 is equal to
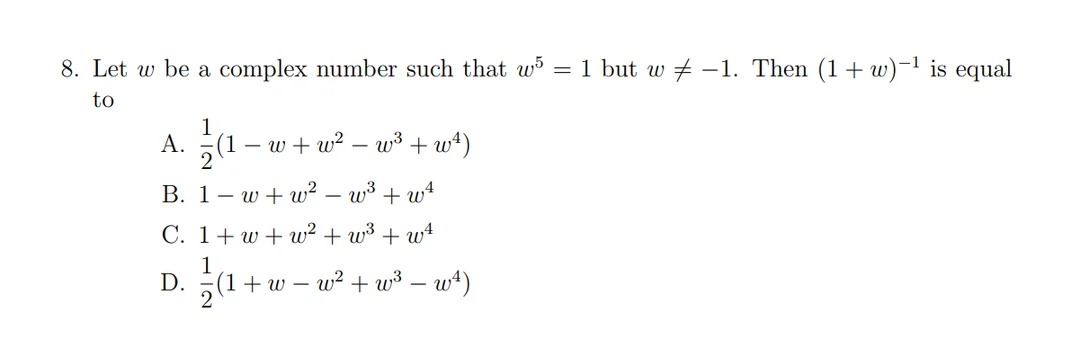
21(1−w+w2−w3+w4)
1−w+w2−w3+w4
1+w+w2+w3+w4
21(1+w−w2+w3−w4)
A
Solution
The problem requires finding the value of (1+w)−1 given that w is a complex number satisfying w5=1 and w=−1.
The condition w5=1 indicates that w is a fifth root of unity. The roots of the equation z5−1=0 are given by wk=ei52πk for k=0,1,2,3,4. These roots are 1,ei2π/5,ei4π/5,ei6π/5,ei8π/5. The condition w=−1 is satisfied by all fifth roots of unity, as (−1)5=−1=1.
We can factor the polynomial w5−1 as (w−1)(w4+w3+w2+w+1)=0.
If w=1, then (1+w)−1=(1+1)−1=21. Let's check the options for w=1: A. 21(1−1+12−13+14)=21(1)=21. B. 1−1+12−13+14=1. C. 1+1+12+13+14=5. D. 21(1+1−12+13−14)=21(1)=21. Both A and D yield 21 when w=1.
If w=1, then w is one of the other four fifth roots of unity, and it satisfies w4+w3+w2+w+1=0.
Consider option A: 21(1−w+w2−w3+w4). This expression is 21 times the sum of a geometric series with first term 1, ratio −w, and 5 terms: Sum =1−(−w)1⋅(1−(−w)5)=1+w1−(−w5). Since w5=1, the sum is 1+w1−(−1)=1+w2. Therefore, 21(1−w+w2−w3+w4)=21(1+w2)=(1+w)−1. This confirms that option A is correct for all w such that w5=1.
Consider option D: 21(1+w−w2+w3−w4). Let's multiply (1+w) by this expression: (1+w)⋅21(1+w−w2+w3−w4) =21[(1+w)(1+w−w2+w3−w4)] =21[1(1+w−w2+w3−w4)+w(1+w−w2+w3−w4)] =21[(1+w−w2+w3−w4)+(w+w2−w3+w4−w5)] =21[1+(w+w)+(−w2+w2)+(w3−w3)+(−w4+w4)−w5] =21[1+2w−w5] Since w5=1, this simplifies to 21[1+2w−1]=21[2w]=w. For this to be equal to (1+w)−1, we would need w=(1+w)−1, which implies w(1+w)=1, so w+w2=1. This is not generally true for all fifth roots of unity. However, if we want 21(1+w−w2+w3−w4) to be equal to (1+w)−1, then we need w=(1+w)−1, which means w(1+w)=1. This is only true if w=1 (since 1+12=2=1, this is actually not true even for w=1).
Let's re-evaluate the product for option D: (1+w)×21(1+w−w2+w3−w4)=21(1+2w−w5)=21(1+2w−1)=w. So, (1+w)−1=w1×21(1+w−w2+w3−w4). For option D to be correct, we need 21(1+w−w2+w3−w4)=(1+w)−1. This means w1×21(1+w−w2+w3−w4)=21(1+w−w2+w3−w4), which implies w1=1, or w=1. Thus, option D is only correct when w=1.
Since option A is correct for all valid values of w, it is the correct answer for this single-choice question.
