Question

Let L₁: $\overrightarrow{r}$ = ($\hat{i}$-$\hat{j}$+2$\hat{k}$)+$\lambda$($\hat{i}$-$\hat{j}$+2$\hat{k}$), $\lambda \epsilon$R L₂: $\overrightarrow{r}$ = ($\hat{j}$-$\hat{k}$)+$\mu$(3$\hat{i}$+$\hat{j}$+p$\hat{k}$), $\mu \epsilon$ R, and L₃: $\overrightarrow{r}$ = $\delta$(l$\hat{i}$+m$\hat{j}$+n$\hat{k}$), $\delta \epsilon$ R be three lines such that L₁ is perpendicular to L₂ and L₃ is perpendicular to both L₁ and L₂. Then, the point which lies on L₃ is

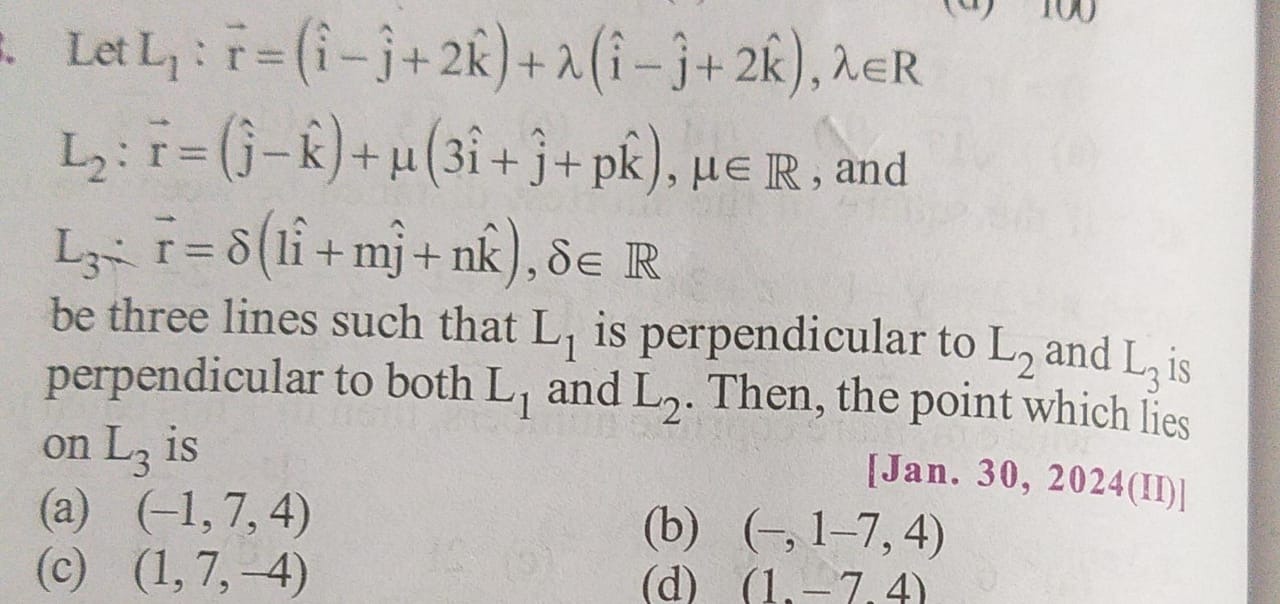
• A. (-1, 7, 4)
• B. (-, 1-7, 4)
• C. (1, 7, -4)
• D. (1.-7.4)

Answer 1

Answer: (A)

(-1, 7, 4)

Answer 2

The direction vector of L₁ is $\overrightarrow{b_1} = \hat{i}-\hat{j}+2\hat{k}$. The direction vector of L₂ is $\overrightarrow{b_2} = 3\hat{i}+\hat{j}+p\hat{k}$. Since L₁ ⊥ L₂, $\overrightarrow{b_1} \cdot \overrightarrow{b_2} = 0$. This gives $3 - 1 + 2p = 0$, so $p = -1$. Thus, $\overrightarrow{b_2} = 3\hat{i}+\hat{j}-\hat{k}$. The direction vector of L₃, $\overrightarrow{b_3} = l\hat{i}+m\hat{j}+n\hat{k}$, is perpendicular to both L₁ and L₂. Thus, $\overrightarrow{b_3}$ is parallel to $\overrightarrow{b_1} \times \overrightarrow{b_2}$. $\overrightarrow{b_1} \times \overrightarrow{b_2} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -1 & 2 \\ 3 & 1 & -1 \end{vmatrix} = \hat{i}(1-2) - \hat{j}(-1-6) + \hat{k}(1+3) = -\hat{i} + 7\hat{j} + 4\hat{k}$. So, L₃ has the direction vector $(-1, 7, 4)$. Since L₃ passes through the origin, its equation is $\overrightarrow{r} = t(-\hat{i} + 7\hat{j} + 4\hat{k})$. Checking the options, (-1, 7, 4) corresponds to $t=1$ and lies on L₃.