Question
Question: $\left(\frac{3^{x-2}}{3^x-2^x}\right)>1+\left(\frac{2}{3}\right)^x$...
(3x−2x3x−2)>1+(32)x
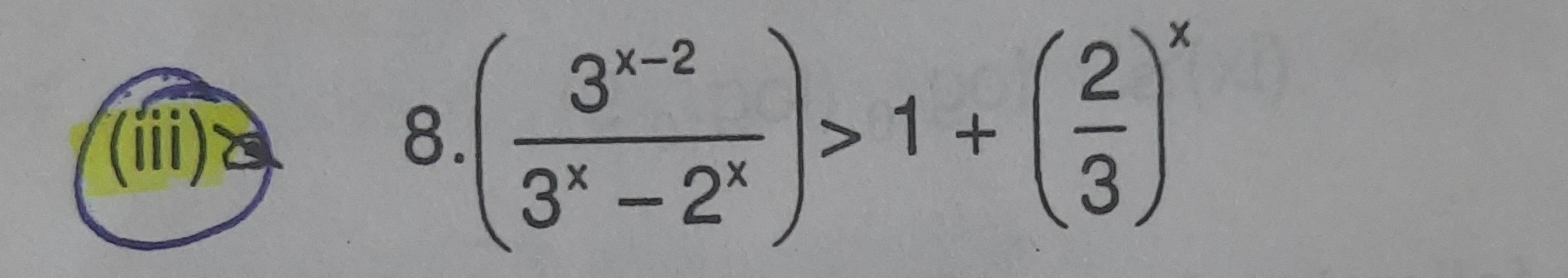
(0,log2/3(322))
Solution
The given inequality is (3x−2x3x−2)>1+(32)x.
First, simplify the left side: 3x−2x3x−2=3x(1−3x2x)3x⋅3−2=1−(32)x3−2=1−(32)x1/9.
Let y=(32)x. Since 2/3>0, y>0 for all real x. The inequality becomes: 1−y1/9>1+y.
The denominator 1−y cannot be zero, so y=1. This means (32)x=1, which implies x=0.
Rearrange the inequality: 1−y1/9−(1+y)>0 1−y1/9−(1+y)(1−y)>0 1−y1/9−(1−y2)>0 1−y1/9−1+y2>0 1−yy2−8/9>0 1−y(y−8/3)(y+8/3)>0 1−y(y−22/3)(y+22/3)>0.
Since y=(2/3)x>0, the term (y+22/3) is always positive. We can divide the inequality by this term without changing the sign: 1−yy−22/3>0.
This inequality holds if and only if the numerator and denominator have the same sign.
Case 1: y−22/3>0 and 1−y>0. y>22/3 and y<1. So, 22/3<y<1.
Case 2: y−22/3<0 and 1−y<0. y<22/3 and y>1. Since 22/3=8/9<1=1, the condition y>1 and y<22/3 has no solution.
So the only solution for y is 22/3<y<1.
Substitute back y=(32)x: 22/3<(32)x<1.
This inequality can be split into two parts:
-
(32)x<1 Since 1=(32)0 and the base 2/3 is between 0 and 1, the function (32)x is decreasing. (32)x<(32)0⟹x>0.
-
22/3<(32)x Let x0=log2/3(22/3). This is the value of x for which (32)x=22/3. So the inequality is (32)x0<(32)x. Since the base 2/3 is between 0 and 1, the inequality sign flips when comparing the exponents: x0>x.
Combining the two conditions x>0 and x<x0, we get 0<x<x0.
The value of x0 is log2/3(22/3). We can write 22/3=23/2⋅3−1. x0=log2/3(23/2⋅3−1)=ln(2/3)ln(23/2⋅3−1)=ln2−ln323ln2−ln3.
The solution set for x is (0,log2/3(22/3)).
The final answer is (0,log2/3(322)).
Explanation of the solution:
- Simplify the given inequality by expressing terms with a common base (2/3)x.
- Introduce a substitution y=(2/3)x to transform the inequality into a rational inequality in terms of y.
- Solve the rational inequality for y, considering the constraint y>0 (since y=(2/3)x).
- Convert the solution for y back into terms of x using y=(2/3)x.
- Solve the resulting exponential inequalities for x, taking into account that the base 2/3 is less than 1, which reverses the inequality direction when comparing exponents.
- Combine the solutions from the exponential inequalities to find the final range for x. The logarithm base 2/3 is used to express the boundary value.
Answer: The solution is the interval (0,log2/3(322)). This corresponds to the range 0<x<log2/3(322).
