Question
Question: In the circuit shown in the figure, $R_{AB}=?$ ...
In the circuit shown in the figure,
RAB=?
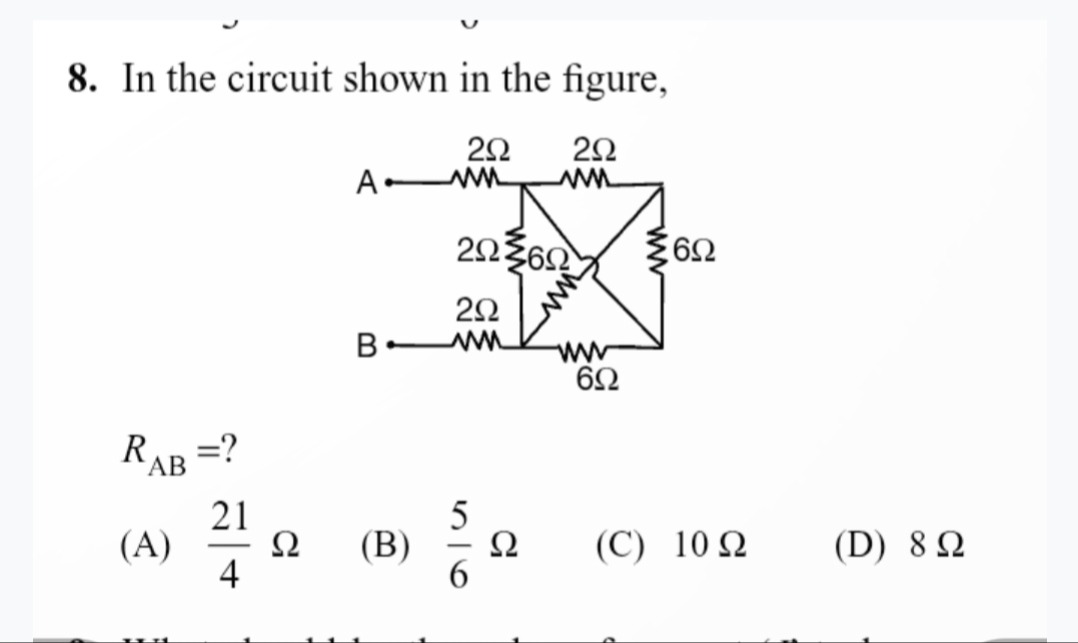
421 Ω
65 Ω
10 Ω
8 Ω
421 Ω
Solution
-
Identify the circuit type: The circuit contains a bridge-like structure CDEF with two diagonals RCF (6Ω) and RDE (6Ω).
-
Check for balanced Wheatstone bridge: Consider the bridge C-D-F-E with RDE as the central resistor. The arms are RCD=2Ω, RDF=6Ω, RCE=2Ω, REF=6Ω.
The condition for a balanced bridge (no current through RDE) is RDFRCD=REFRCE.
Substituting the values: 62=62, which simplifies to 31=31.
Since the condition is met, the bridge is balanced. This means the potential at node D is equal to the potential at node E (VD=VE).
-
Simplify the circuit by removing the balanced arm and merging nodes: Since VD=VE, no current flows through the 6Ω resistor between D and E. This resistor can be removed. Furthermore, since D and E are at the same potential, they can be merged into a single node, let's call it D'.
-
Redraw the simplified circuit and calculate equivalent resistances:
-
The 2Ω resistor (RCD) and 2Ω resistor (RCE) are now in parallel between C and D'.
RCD′=2+22×2=1Ω.
-
The 6Ω resistor (RDF) and 6Ω resistor (REF) are now in parallel between D' and F.
RD′F=6+66×6=3Ω.
-
The 6Ω resistor (RCF) remains connected between C and F.
The circuit now consists of:
- RAC=2Ω
- RBD′=2Ω
- RCD′=1Ω
- RD′F=3Ω
- RCF=6Ω
-
-
Apply Nodal Analysis: Let VB=0 and VA=V. Let VC,VD′,VF be the potentials at nodes C, D', F respectively.
-
Node C: 2VA−VC=1VC−VD′+6VC−VF
Multiplying by 6: 3(VA−VC)=6(VC−VD′)+(VC−VF)
3VA=10VC−6VD′−VF (Eq. 1)
-
Node D': 1VC−VD′=2VD′−VB+3VD′−VF
Multiplying by 6: 6(VC−VD′)=3(VD′−0)+2(VD′−VF)
6VC=11VD′−2VF (Eq. 2)
-
Node F: 6VC−VF+3VD′−VF=0
Multiplying by 6: (VC−VF)+2(VD′−VF)=0
VC+2VD′=3VF (Eq. 3)
-
-
Solve the system of equations:
From Eq. 3: VF=3VC+2VD′
Substitute VF into Eq. 2:
6VC=11VD′−2(3VC+2VD′)
18VC=33VD′−2VC−4VD′
20VC=29VD′⟹VD′=2920VC
Substitute VD′ into VF:
VF=3VC+2(2920VC)=3VC(1+2940)=3VC(2969)=2923VC
Substitute VD′ and VF into Eq. 1:
3VA=10VC−6(2920VC)−2923VC
3VA=VC(10−29120−2923)=VC(29290−120−23)=VC(29147)
VC=1473×29VA=14787VA=4929VA
-
Calculate the total current and equivalent resistance:
The total current flowing from A to B is IAB=IAC=2VA−VC.
IAB=2VA−4929VA=2VA(4949−29)=2VA(4920)=4910VA.
The equivalent resistance RAB=IABVA−VB=IABVA−0=4910VAVA=1049=4.9Ω.
-
Compare with options:
(A) 421=5.25Ω (B) 65≈0.83Ω (C) 10Ω (D) 8Ω
The calculated value 4.9Ω is closest to option (A) 5.25Ω.
The final answer is A
