Question

In the circuit shown in figure, the current through 4Ω resistance is

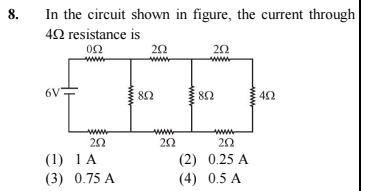
• A. 1 A
• B. 0.25 A
• C. 0.75 A
• D. 0.5 A

Answer 1

Answer: (D)

0.5 A

Answer 2

To find the current through the 4Ω resistor, we can apply Kirchhoff's Laws and nodal analysis.

1. Node Definition: Assign node potentials, setting the negative terminal of the battery as 0V. The node after the 0Ω resistor at the top is 6V.
2. KCL Equations: Write Kirchhoff's Current Law equations for the unknown nodes (V_B, V_C, V_D, V_E, V_F).
   • $9V_B - 4V_C - V_E = 24$
   • $-2V_B + 3V_C - V_F = 0$
   • $9V_D - 4V_E = 6$
   • $-V_B - 4V_D + 9V_E - 4V_F = 0$
   • $-V_C - 2V_E + 5V_F = 0$
3. Solve System of Equations: Solve the system of linear equations to find the node potentials.
   • From the equations, express $V_E$ and $V_F$ in terms of $V_B$ and $V_C$.
     • $V_E = 7V_C - 5V_B$
     • $V_F = 3V_C - 2V_B$
   • Substitute these into the remaining equations to reduce the system to 3 unknowns ($V_B$, $V_C$, $V_D$).
     • $14V_B - 11V_C = 24$
     • $20V_B - 28V_C + 9V_D = 6$
     • $-38V_B + 51V_C - 4V_D = 0$
   • Further reduce to 2 unknowns ($V_B$, $V_D$):
     • $74V_B - 11V_D = 306$
     • $-172V_B + 99V_D = -606$
   • Solve for $V_B$: $V_B = \frac{2148}{494} = \frac{1074}{247}$ V.
4. Calculate $V_C$ and $V_F$:
   • $V_C = \frac{14V_B - 24}{11} = \frac{9108}{2717}$ V.
   • $V_F = 3V_C - 2V_B = \frac{3696}{2717}$ V.
5. Calculate Current: The current through the 4Ω resistor is $I_{4\Omega} = \frac{V_C - V_F}{4}$.
   • $I_{4\Omega} = \frac{\frac{9108}{2717} - \frac{3696}{2717}}{4} = \frac{5412}{2717 \times 4} = \frac{5412}{10868} = \frac{1353}{2717}$ A.
6. Approximate to nearest option: $\frac{1353}{2717} \approx 0.497975$ A, which is approximately 0.5 A.