Question
Question: If $L = \lim_{x \to 1} \frac{(1-x)(1-x^2)(1-x^3)....(1-x^{2n})}{[(1-x)(1-x^2)(1-x^3)....(1-x^n)]^2}$...
If L=limx→1[(1−x)(1−x2)(1−x3)....(1−xn)]2(1−x)(1−x2)(1−x3)....(1−x2n) then L can be equal to
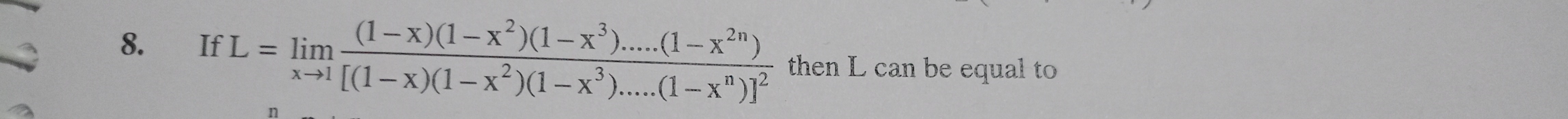
(n2n)
Solution
The given limit is L=limx→1[(1−x)(1−x2)(1−x3)....(1−xn)]2(1−x)(1−x2)(1−x3)....(1−x2n).
We can rewrite the term (1−xk) using the factorization 1−xk=(1−x)(1+x+x2+...+xk−1).
Let the numerator be N(x)=∏k=12n(1−xk). Using the factorization, N(x)=∏k=12n[(1−x)(1+x+...+xk−1)]. N(x)=(1−x)2n∏k=12n(1+x+...+xk−1).
Let the denominator be D(x)=[∏k=1n(1−xk)]2. Using the factorization, ∏k=1n(1−xk)=∏k=1n[(1−x)(1+x+...+xk−1)]. ∏k=1n(1−xk)=(1−x)n∏k=1n(1+x+...+xk−1). So, D(x)=[(1−x)n∏k=1n(1+x+...+xk−1)]2=(1−x)2n[∏k=1n(1+x+...+xk−1)]2.
Now substitute these back into the expression for L: L=limx→1(1−x)2n[∏k=1n(1+x+...+xk−1)]2(1−x)2n∏k=12n(1+x+...+xk−1).
We can cancel the (1−x)2n terms, assuming x=1: L=limx→1[∏k=1n(1+x+...+xk−1)]2∏k=12n(1+x+...+xk−1).
Now, we evaluate the limit of each term (1+x+...+xk−1) as x→1. limx→1(1+x+...+xk−1)=1+1+...+1 (k times) =k.
Since the limit of each factor exists and is finite, the limit of the product is the product of the limits. The numerator limit is ∏k=12n(limx→1(1+x+...+xk−1))=∏k=12nk=1⋅2⋅3⋅...⋅(2n)=(2n)!.
The denominator limit is [∏k=1n(limx→1(1+x+...+xk−1))]2=[∏k=1nk]2=[1⋅2⋅3⋅...⋅n]2=(n!)2.
So, the limit L is: L=(n!)2(2n)!.
This expression is the definition of the binomial coefficient (n2n). L=(n2n).
