Question

If given arrangement is moving towards left with speed v, then potential difference between B and D and current in the loop are respectively :-

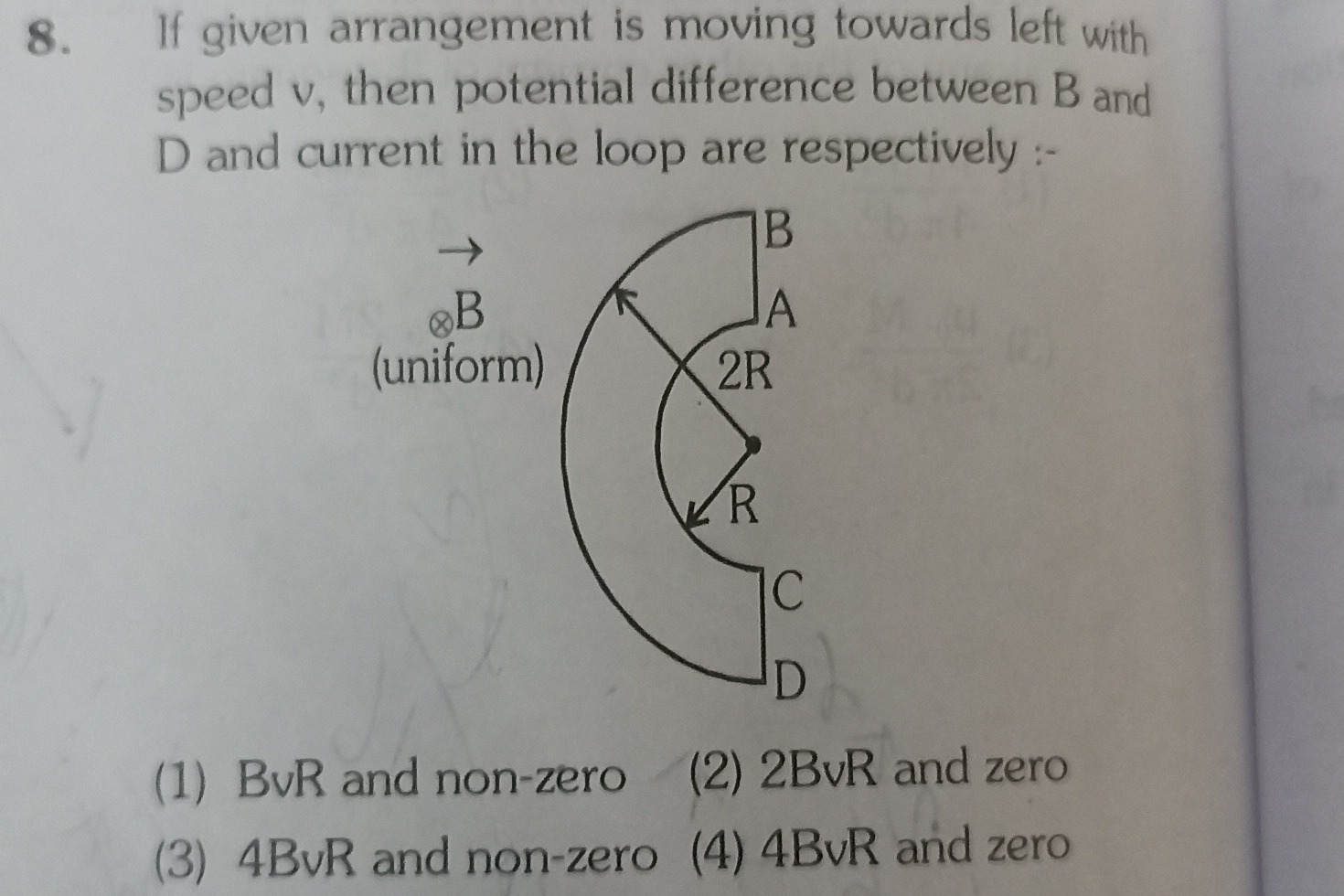
• A. BvR and non-zero
• B. 2BvR and zero
• C. 4BvR and non-zero
• D. 4BvR and zero

Answer 1

Answer: (B)

2BvR and zero

Answer 2

The problem describes a C-shaped conductor moving to the left with velocity $\vec{v}$ in a uniform magnetic field $\vec{B}$ directed into the page. We need to find the potential difference between points B and D, and the current in the loop.

Let's set up a coordinate system:

• Velocity of the arrangement: $\vec{v} = -v\hat{i}$ (moving to the left).
• Magnetic field: $\vec{B} = -B\hat{k}$ (into the page).

The motional EMF induced across a conductor segment $d\vec{l}$ is $d\mathcal{E} = (\vec{v} \times \vec{B}) \cdot d\vec{l}$.

First, let's calculate the term $(\vec{v} \times \vec{B})$: $\vec{v} \times \vec{B} = (-v\hat{i}) \times (-B\hat{k}) = vB(\hat{i} \times \hat{k}) = vB(-\hat{j})$.

So, the induced electric field (and the force on positive charges) is directed downwards, in the negative y-direction.

The potential difference $V_{P_2} - V_{P_1}$ across a segment from $P_1$ to $P_2$ is given by $V_{P_2} - V_{P_1} = -\int_{P_1}^{P_2} (\vec{v} \times \vec{B}) \cdot d\vec{l}$.

Substituting $(\vec{v} \times \vec{B}) = -vB\hat{j}$, we get: $V_{P_2} - V_{P_1} = -\int_{P_1}^{P_2} (-vB\hat{j}) \cdot d\vec{l} = vB \int_{P_1}^{P_2} \hat{j} \cdot d\vec{l}$.

This means that only the vertical component of the displacement contributes to the potential difference.

Let's analyze each segment of the loop:

1. Segment AB: This is a straight vertical conductor. From the diagram, B is above A. The length of this segment is the difference between the outer radius (2R) and inner radius (R), so $L_{AB} = 2R - R = R$. The displacement vector $d\vec{l}$ for going from A to B is in the positive y-direction ($dy\hat{j}$). $V_B - V_A = vB \int_A^B \hat{j} \cdot (dy\hat{j}) = vB \int_A^B dy = vB R$. So, $V_B = V_A + BvR$. (B is at higher potential than A).

2. Segment CD: This is also a straight vertical conductor. From the diagram, C is above D. The length of this segment is $L_{CD} = 2R - R = R$. The displacement vector $d\vec{l}$ for going from D to C is in the positive y-direction ($dy\hat{j}$). $V_C - V_D = vB \int_D^C \hat{j} \cdot (dy\hat{j}) = vB \int_D^C dy = vB R$. So, $V_C = V_D + BvR$. (C is at higher potential than D).

3. Arc AC (Inner Arc): This is a curved conductor. The diagram shows it as a horizontal arc connecting A and C. For any segment $d\vec{l}$ along this horizontal arc, $d\vec{l}$ is tangential and therefore horizontal. Since $\hat{j} \cdot d\vec{l} = 0$ for a horizontal $d\vec{l}$, the potential difference $V_C - V_A = 0$. Therefore, $V_A = V_C$.

4. Arc DB (Outer Arc): This is also a curved conductor, shown as a horizontal arc connecting D and B. Similar to arc AC, for any segment $d\vec{l}$ along this horizontal arc, $d\vec{l}$ is horizontal. Thus, the potential difference $V_B - V_D = 0$. Therefore, $V_B = V_D$.

Potential difference between B and D: From our calculation for Arc DB, we found $V_B - V_D = 0$.

Current in the loop: Let's trace the potential around the loop, say starting from D and going counter-clockwise (D -> C -> A -> B -> D).

• $V_C - V_D = BvR$
• $V_A - V_C = 0$
• $V_B - V_A = BvR$
• $V_D - V_B = 0$

Summing the potential changes around the loop: $(V_C - V_D) + (V_A - V_C) + (V_B - V_A) + (V_D - V_B) = BvR + 0 + BvR + 0 = 2BvR$.

The net induced EMF in the closed loop is $\oint \vec{E}_{ind} \cdot d\vec{l} = \oint (\vec{v} \times \vec{B}) \cdot d\vec{l}$.

Let's calculate the total EMF by summing the EMFs of the segments: $\mathcal{E}_{loop} = \mathcal{E}_{DC} + \mathcal{E}_{CA} + \mathcal{E}_{AB} + \mathcal{E}_{BD}$ (assuming positive direction is D to C to A to B to D). $\mathcal{E}_{DC} = V_C - V_D = BvR$. $\mathcal{E}_{CA} = V_A - V_C = 0$. $\mathcal{E}_{AB} = V_B - V_A = BvR$. $\mathcal{E}_{BD} = V_D - V_B = 0$.

Total EMF = $BvR + 0 + BvR + 0 = 2BvR$.

Since the total induced EMF in the closed loop is $2BvR$ (which is non-zero), there will be a current flowing in the loop.

Therefore, the potential difference between B and D is zero, and the current in the loop is non-zero.

However, a common interpretation in such problems is to assume the loop is open at B and D when measuring the potential difference.

If the loop is open at B and D, then the current in the loop is zero. In this case, the potential difference $V_B - V_D$ would be the EMF induced along the path D-C-A-B, which is $2BvR$.

So, $V_B - V_D = 2BvR$ and current in the loop = 0.