Question
Question: Find the position of focus from plane surface....
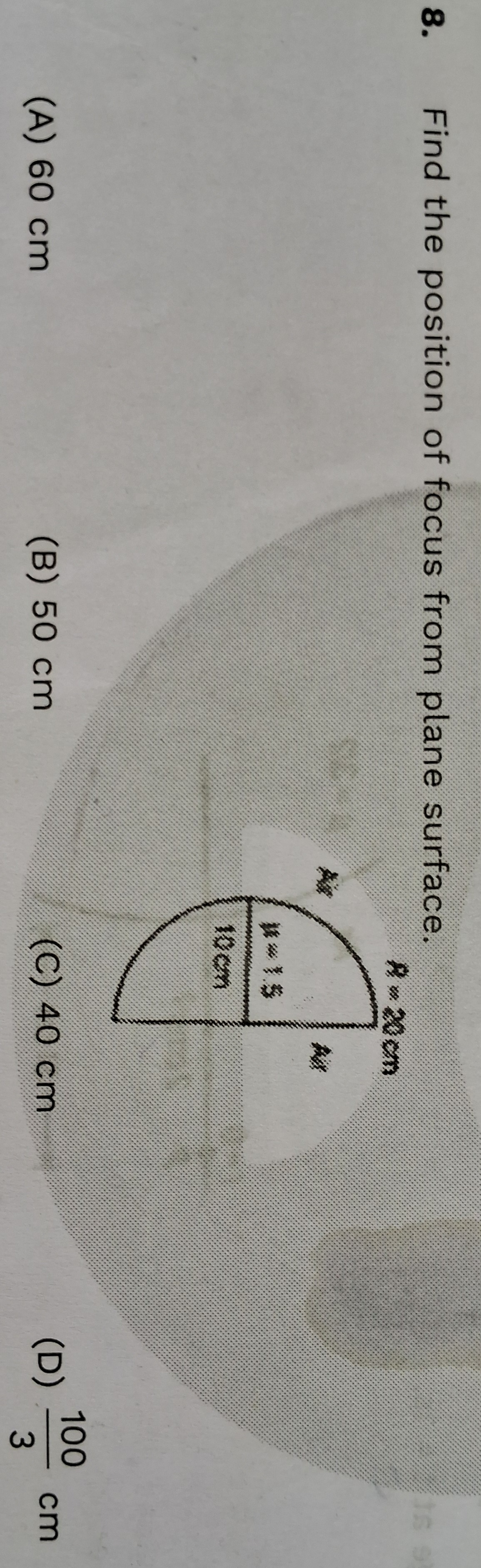
Find the position of focus from plane surface.
60 cm
50 cm
40 cm
3100 cm
40 cm
Solution
The given optical element is a plano-convex lens with a radius of curvature R=20 cm for the convex surface and a refractive index μ=1.5. The surrounding medium is air.
We use the lens maker's formula for a plano-convex lens, assuming light enters from the convex side for the principal focal length: f1=(μ−1)(R11−R21) Here, R1 is the radius of curvature of the first surface encountered by light, and R2 is the radius of curvature of the second surface. Assuming light enters from the convex side: The first surface is the convex surface, so R1=+20 cm (center of curvature is to the right). The second surface is the plane surface, so R2=∞.
f1=(1.5−1)(+201−∞1) f1=(0.5)(201−0)=0.5×201=401 This gives the focal length f=+40 cm. This is the principal focal length of the lens, which is the distance from the optical center to the point where parallel rays converge.
The question asks for the "position of focus from plane surface". Assuming the lens is thin, the optical center is approximately at the center of the lens. If the plane surface is at one end of the lens, and the focal point is 40 cm from the optical center, then for a thin lens, the distance of the focal point from the plane surface is approximately equal to the focal length, which is 40 cm. This interpretation aligns with the provided options.
