Question
Question: Find the moment of inertia of a uniform square plate of mass M, edge of length $l$ about it passing ...
Find the moment of inertia of a uniform square plate of mass M, edge of length l about it passing through P and perpendicular to it.
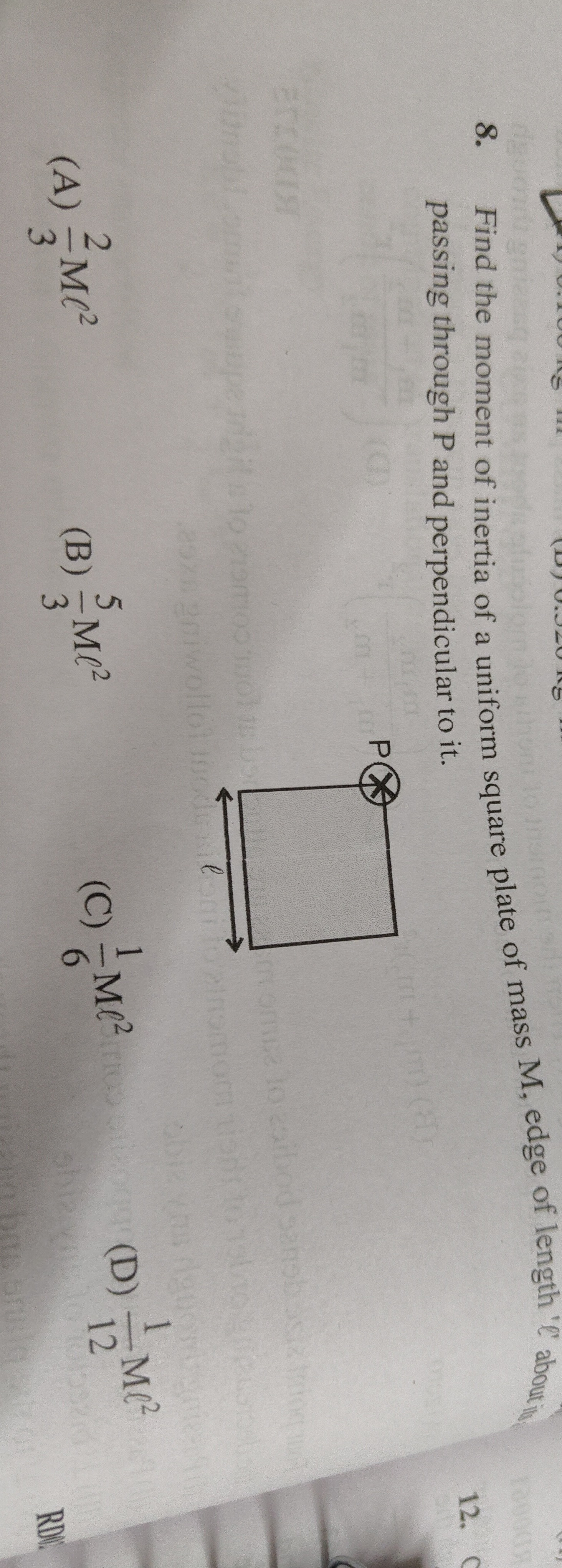
32Ml2
35Ml2
61Ml2
121Ml2
32Ml2
Solution
To find the moment of inertia of a uniform square plate of mass M and edge length l about an axis passing through a corner P and perpendicular to the plate, we can use the parallel axis theorem.
1. Moment of Inertia about the Center of Mass (IC):
First, we need the moment of inertia of the square plate about an axis passing through its center of mass (C) and perpendicular to its plane.
For a uniform square plate of mass M and side length l, the moment of inertia about an axis passing through its center and parallel to one of its sides is 121Ml2.
According to the perpendicular axis theorem, if Ix and Iy are the moments of inertia about two perpendicular axes lying in the plane of the body and passing through the center of mass, then the moment of inertia about an axis perpendicular to the plane and passing through the intersection of Ix and Iy is Iz=Ix+Iy.
For a square plate, Ix=Iy=121Ml2.
Therefore, the moment of inertia about an axis passing through the center of mass C and perpendicular to the plane is: IC=Ix+Iy=121Ml2+121Ml2=122Ml2=61Ml2.
2. Distance between the Center of Mass and Point P:
Point P is a corner of the square plate. The center of mass C is at the geometric center of the square.
The coordinates of the center C can be taken as (0,0). The coordinates of a corner P can be taken as (l/2,l/2).
The distance d between the center of mass C and the corner P is: d=(2l)2+(2l)2=4l2+4l2=42l2=2l2=2l.
3. Applying the Parallel Axis Theorem:
The parallel axis theorem states that IP=IC+Md2, where IP is the moment of inertia about the axis passing through P, IC is the moment of inertia about a parallel axis passing through the center of mass, M is the total mass, and d is the perpendicular distance between the two parallel axes.
Substituting the values we found: IP=61Ml2+M(2l)2 IP=61Ml2+M(2l2) IP=61Ml2+21Ml2
To add these fractions, find a common denominator, which is 6:
IP=61Ml2+63Ml2 IP=61+3Ml2 IP=64Ml2 IP=32Ml2
