Question
Question: Correct order of bond angles in the given compounds is/are:...
Correct order of bond angles in the given compounds is/are:
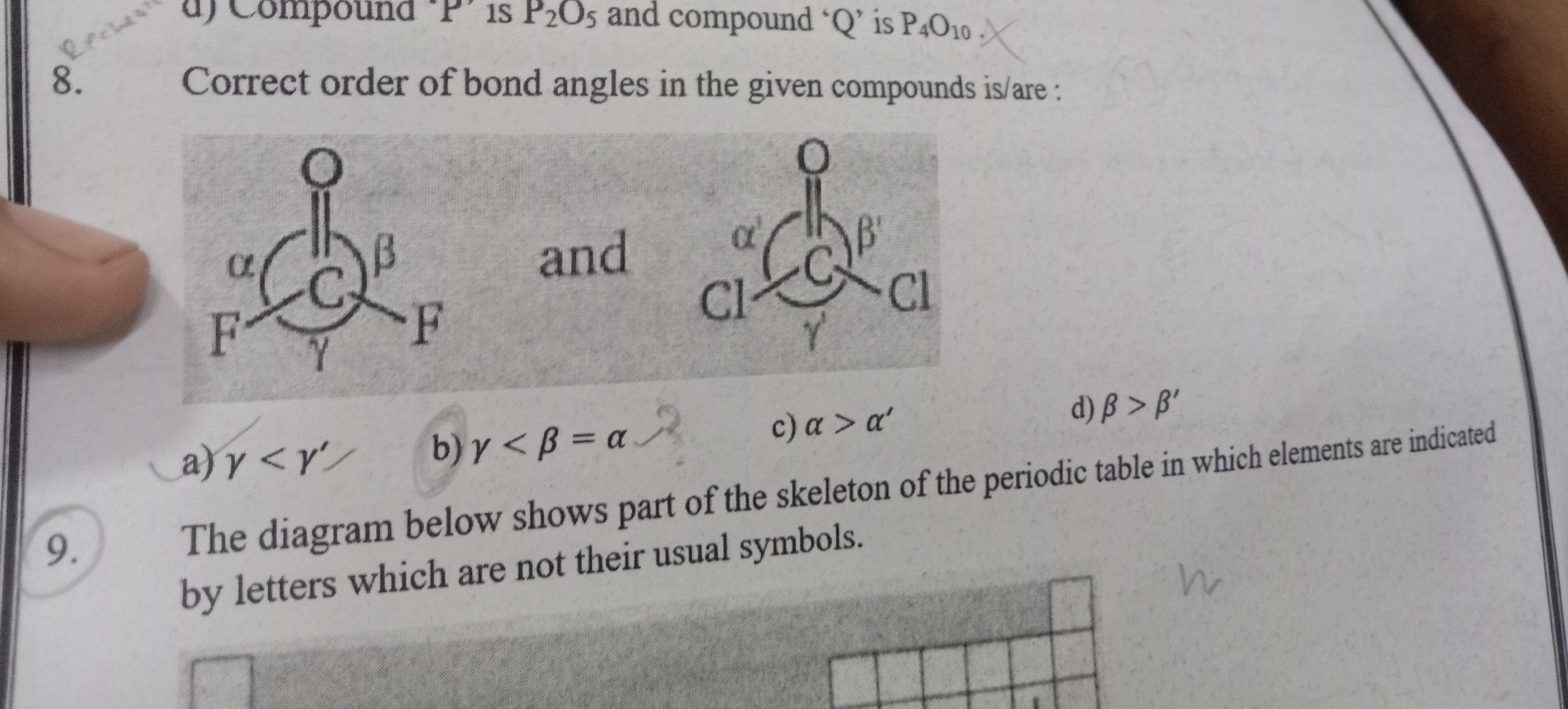
γ<γ′
γ<β=α
α>α′
β>β′
a, b
Solution
In molecules with trigonal planar geometry around the central carbon atom, bond angles are influenced by the presence of double bonds and the electronegativity of substituents. A double bond exerts greater electron repulsion than a single bond, leading to larger angles between the double bond and single bonds, and smaller angles between single bonds. More electronegative substituents withdraw electron density, reducing repulsion, while less electronegative substituents donate electron density, increasing repulsion.
For a molecule like CF2=O, assuming the angles are labeled such that α and β are the angles between C=O and C-F, and γ is the angle between the two C-F bonds, the stronger repulsion from the double bond causes α=β>γ. This supports option (b) γ<β=α.
For a molecule like CFCl=O, let α′ be the angle between C=O and C-Cl, β′ be the angle between C=O and C-F, and γ′ be the angle between C-Cl and C-F. Given that the electronegativity of Fluorine (3.98) is greater than Chlorine (3.16), the repulsion order is C=O > C-Cl > C-F. Consequently, the angle between C=O and C-Cl (α′) will be larger than the angle between C=O and C-F (β′), meaning α′>β′. Also, the angle between C-Cl and C-F (γ′) is expected to be larger than the angle between two C-F bonds (γ) in CF2=O because Chlorine exerts more repulsion than Fluorine. Thus, γ′>γ, supporting option (a) γ<γ′.
Evaluating the options: a) γ<γ′: Correct, as γ′ is expected to be larger than γ. b) γ<β=α: Correct, based on the analysis of CF2=O. c) α>α′: Incorrect, as α′>α because C-Cl repulsion is greater than C-F repulsion. d) β>β′: Incorrect, as β and β′ are angles between C=O and C-F in CF2=O and CFCl=O respectively. Due to differences in the other substituent (F vs Cl), these angles are not necessarily equal and β>β′ is not universally true, and in fact, the C=O bond's influence is moderated by the other substituent. A more detailed analysis would show β≈β′ or β′>β depending on subtle effects, but β>β′ is not the correct general statement. The primary comparison is between the angles formed by different bonds.
