Question
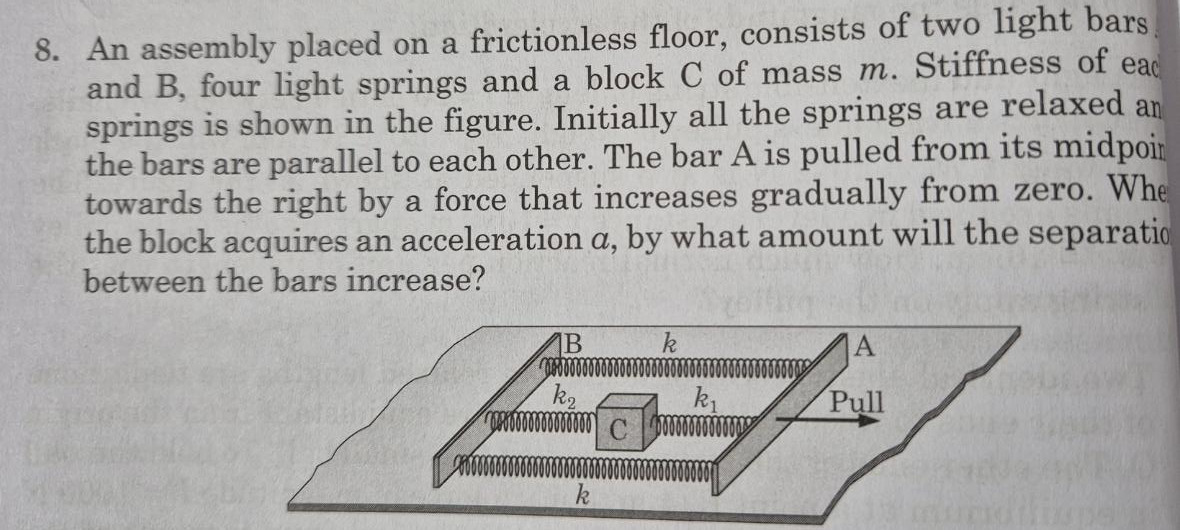
Question: 8. An assembly placed on a frictionless floor, consists of two light bars and B, four light springs ...
- An assembly placed on a frictionless floor, consists of two light bars and B, four light springs and a block C of mass m. Stiffness of each springs is shown in the figure. Initially all the springs are relaxed and the bars are parallel to each other. The bar A is pulled from its midpoint towards the right by a force that increases gradually from zero. When the block acquires an acceleration α, by what amount will the separation between the bars increase?
\Delta=\frac{m\alpha}{2k+\frac{k_1k_2}{k_1+k_2}}.
Solution
We note that the two bars are connected by two “branches” of springs. One branch is the pair of “direct” springs (one at the top and one at the bottom) both with stiffness k acting in parallel so that their combined stiffness is
Kdirect=2k.The other branch is through the block C (of mass m) which is connected to bar A by a spring of stiffness k1 and to bar B by a spring of stiffness k2. These two springs act in series so that their effective stiffness is
Kseries=k1+k2k1k2.Since the two branches are in parallel (that is, they both contribute to holding the two bars together) the net effective stiffness of the connection is
Keff=2k+k1+k2k1k2.When the assembly is accelerated, the block C experiences an inertial force mα (in the opposite direction in a coaccelerating frame). In order to “support” this inertial load the springs must stretch and cause an increase Δ in the separation between the bars. By Hooke’s law we have
KeffΔ=mα,and hence
Δ=2k+k1+k2k1k2mα.