Question

A solid weightless rod of length 2L rests with end A on a smooth vertical wall, and with end B on a horizontal rough surface. The coefficient of friction between the rod and the horizontal surface is $\mu$. A small bead of mass m can slide along the rod without friction. The bodies are held so that the rod is located at an angle $a = 45^{\circ}$ to the horizontal, and the bead is in the middle of the rod. The bodies are released, and after some time the rod begins to move, while the bead does not have time to hit the horizontal surface by this point in time. Find the speed of the bead (in m/s) at the moment when the rod begins to move? [Take $\mu = \frac{1}{\sqrt{2}}$, L = 1m]

Answer 1

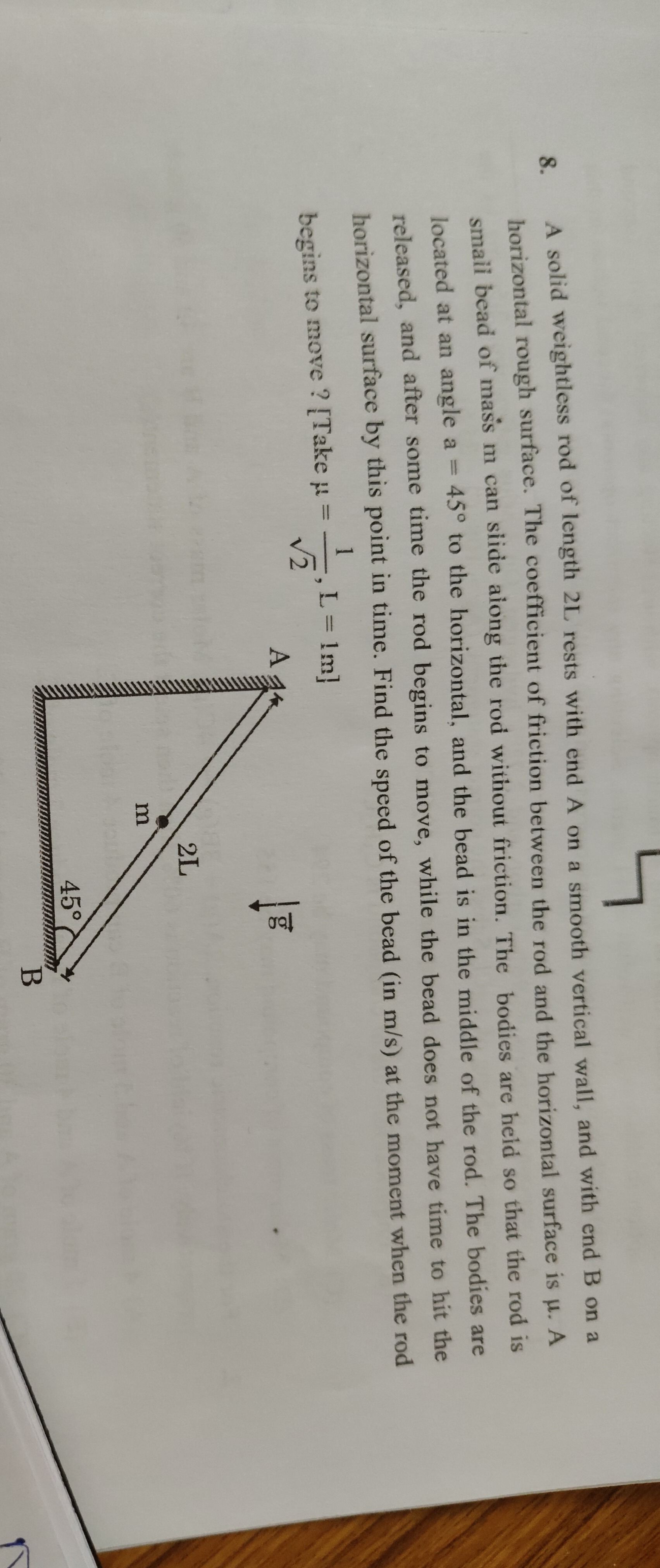
3.16

Answer 2

Explanation of the solution:

1. Identify forces on the bead and rod. The bead's motion along the rod is governed by the component of gravity along the rod, $mg \sin \alpha$. The normal force from the rod on the bead is $N_{br} = mg \cos \alpha$.

2. Apply the work-energy theorem to the bead. As the bead slides down the rod from its initial position (distance $L$ from B) to a new position (distance $r$ from B), its potential energy decreases, converting into kinetic energy. The speed of the bead relative to the rod is $v_b = \sqrt{2g(L-r)\sin\alpha}$.

3. Analyze the forces on the rod to determine the condition for it to start moving. The rod is weightless. Forces are $N_A$ (from wall), $N_B$ (from ground), $f_B$ (friction from ground), and $N_{rb}$ (from bead on rod). $N_{rb}$ is perpendicular to the rod, pointing inwards, with magnitude $mg \cos \alpha$.

4. Resolve $N_{rb}$ into horizontal ($N_{rb,x} = mg \cos \alpha \sin \alpha$, left) and vertical ($N_{rb,y} = mg \cos^2 \alpha$, down) components.

5. Apply equilibrium conditions for the rod just before it moves:

   • Vertical forces: $N_B = N_{rb,y} = mg \cos^2 \alpha$.
   • Torque about B: $N_A (2L \sin \alpha) = N_{rb} r \implies N_A = \frac{mg r \cos \alpha}{2L \sin \alpha}$.

6. Determine the direction of friction. At $\alpha=45^\circ$, initial horizontal force $N_A - N_{rb,x} = 0$. As the bead slides down, $r$ decreases, causing $N_A$ to decrease. Thus, $N_A < N_{rb,x}$, meaning the rod tends to move left, so friction $f_B$ acts right.

7. Apply horizontal force balance: $N_A - N_{rb,x} + f_B = 0 \implies f_B = N_{rb,x} - N_A$.

8. The rod starts moving when $f_B = \mu N_B$. Substitute expressions for $f_B$, $N_A$, $N_{rb,x}$, $N_B$: $mg \cos \alpha \sin \alpha - \frac{mg r \cos \alpha}{2L \sin \alpha} = \mu mg \cos^2 \alpha$. This simplifies to $r = 2L \sin \alpha (\sin \alpha - \mu \cos \alpha)$.

9. Substitute the given values: $\alpha = 45^\circ$, $\mu = 1/\sqrt{2}$, $L = 1$m. $r = 2(1) (1/\sqrt{2}) (1/\sqrt{2} - (1/\sqrt{2})(1/\sqrt{2})) = \sqrt{2} (1/\sqrt{2} - 1/2) = 1 - 1/\sqrt{2}$.

10. Substitute this value of $r$ back into the bead's speed equation: $v_b^2 = 2g (L - r) \sin \alpha = 2g (1 - (1 - 1/\sqrt{2})) (1/\sqrt{2}) = 2g (1/\sqrt{2}) (1/\sqrt{2}) = g$. So, $v_b = \sqrt{g}$.

11. Using $g=10 \text{ m/s}^2$, $v_b = \sqrt{10} \approx 3.16 \text{ m/s}$.