Question

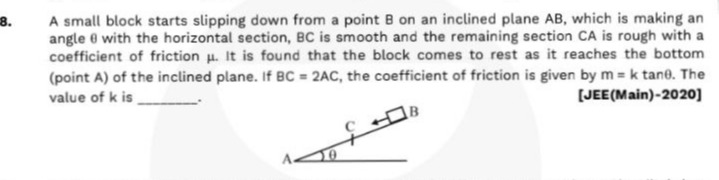
A small block starts slipping down from a point B on an inclined plane AB, which is making an angle $\theta$ with the horizontal section, BC is smooth and the remaining section CA is rough with a coefficient of friction $\mu$. It is found that the block comes to rest as it reaches the bottom (point A) of the inclined plane. If BC = 2AC, the coefficient of friction is given by m = k tan$\theta$. The value of k is _______.

Answer 1

3

Answer 2

The problem can be solved using the Work-Energy Theorem, which states that the net work done on an object is equal to the change in its kinetic energy ($W_{net} = \Delta KE$).

1. Identify Initial and Final States:

• Initial state: Block at point B, starts slipping, so initial velocity $v_B = 0$.
• Final state: Block at point A, comes to rest, so final velocity $v_A = 0$.
• Therefore, the change in kinetic energy $\Delta KE = KE_A - KE_B = \frac{1}{2}mv_A^2 - \frac{1}{2}mv_B^2 = 0 - 0 = 0$.

2. Calculate Work Done by Forces: The forces doing work on the block are gravity and friction.

• Work done by gravity ($W_g$): The block moves from B to A. The vertical height descended is $h_{BA}$. Let the length of section AC be $L$. Given $BC = 2AC$, so $BC = 2L$. The total length of the inclined plane is $AB = AC + BC = L + 2L = 3L$. The vertical height descended is $h_{BA} = AB \sin\theta = (3L) \sin\theta$. Work done by gravity is $W_g = mg h_{BA} = mg (3L \sin\theta)$.

• Work done by friction ($W_f$): Friction acts only on the rough section CA. The length of this section is $L$. The normal force on the inclined plane is $N = mg \cos\theta$. The force of kinetic friction is $f_k = \mu N = \mu mg \cos\theta$. Since friction opposes motion, the work done by friction is negative. $W_f = -f_k \times (\text{distance CA}) = -(\mu mg \cos\theta) L$.

3. Apply Work-Energy Theorem: $W_{net} = W_g + W_f = \Delta KE$ Since $\Delta KE = 0$: $mg (3L \sin\theta) - \mu mg L \cos\theta = 0$

4. Solve for $\mu$: Divide the entire equation by $mgL$ (assuming $m, g, L$ are non-zero): $3 \sin\theta - \mu \cos\theta = 0$ $\mu \cos\theta = 3 \sin\theta$ $\mu = 3 \frac{\sin\theta}{\cos\theta}$ $\mu = 3 \tan\theta$

5. Determine the value of k: The problem states that the coefficient of friction is given by $\mu = k \tan\theta$. Comparing our derived expression for $\mu$ with the given form: $3 \tan\theta = k \tan\theta$ Therefore, $k = 3$.

The final answer is $\boxed{3}$.