Question

A plank of mass $m$ is suspended from two threads, which pass through ideal pulleys and at the other ends of the threads, identical loads each of mass $2m$ placed on the plank are attached. If the setup is in equilibrium, determine the tensile forces in each of the threads, and the forces of normal reactions between the loads and the plank.

Answer 1

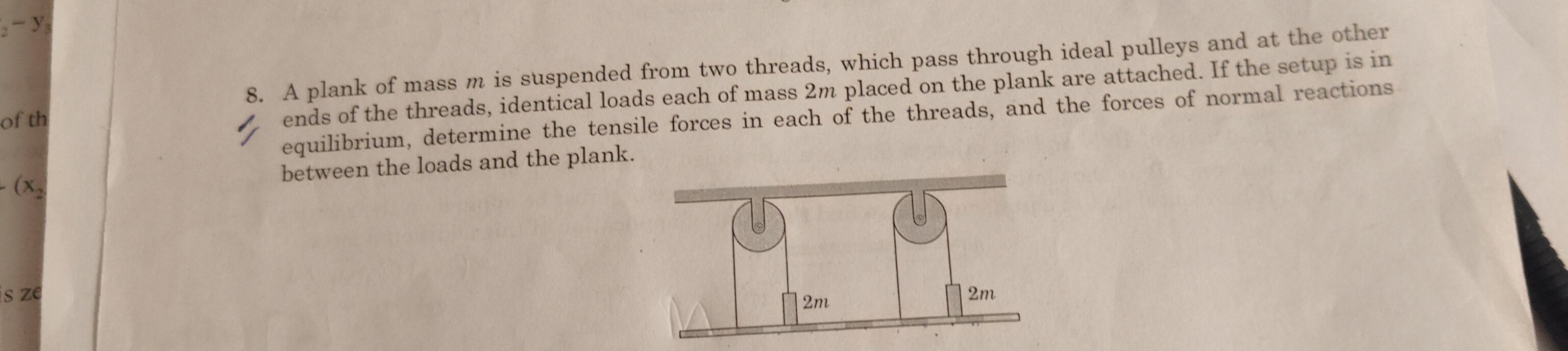
Tension in each thread: $T = \frac{5}{4}mg$, Normal reaction force: $N = \frac{3}{4}mg$

Answer 2

To determine the tensile forces in each thread and the normal reaction forces between the loads and the plank, we will analyze the forces acting on each component using Free Body Diagrams (FBDs) and apply the conditions for equilibrium.

1. Free Body Diagram for one Load (Mass $2m$)

Each load of mass $2m$ is placed on the plank and is also attached to a thread. The forces acting on one such load are:

• Its weight, $W_{load} = (2m)g$, acting vertically downwards.
• The tension, $T$, from the thread, acting vertically upwards.
• The normal reaction force, $N$, from the plank, acting vertically upwards.

Since the load is in equilibrium, the net force in the vertical direction is zero: $\sum F_y = 0 \implies T + N - 2mg = 0$ $T + N = 2mg \quad \text{(Equation 1)}$

2. Free Body Diagram for the Plank (Mass $m$)

The plank of mass $m$ is suspended by two threads and has two loads placed on it. The forces acting on the plank are:

• Its weight, $W_{plank} = mg$, acting vertically downwards.
• The tension, $T$, from the left thread, acting vertically upwards.
• The tension, $T$, from the right thread, acting vertically upwards. (Since the pulleys are ideal and the loads are identical, the tension in both threads will be the same).
• The normal reaction force from the left load, $N$, acting vertically downwards. (By Newton's third law, if the plank exerts an upward normal force $N$ on the load, the load exerts an equal and opposite downward normal force $N$ on the plank).
• The normal reaction force from the right load, $N$, acting vertically downwards.

Since the plank is in equilibrium, the net force in the vertical direction is zero: $\sum F_y = 0 \implies 2T - mg - N - N = 0$ $2T - 2N = mg \quad \text{(Equation 2)}$

3. Solving the System of Equations

We have a system of two linear equations with two unknowns ($T$ and $N$):

1. $T + N = 2mg$
2. $2T - 2N = mg$

From Equation 1, we can express $N$ in terms of $T$: $N = 2mg - T$

Substitute this expression for $N$ into Equation 2: $2T - 2(2mg - T) = mg$ $2T - 4mg + 2T = mg$ $4T = mg + 4mg$ $4T = 5mg$ $T = \frac{5}{4}mg$

Now, substitute the value of $T$ back into the expression for $N$: $N = 2mg - T$ $N = 2mg - \frac{5}{4}mg$ $N = \frac{8}{4}mg - \frac{5}{4}mg$ $N = \frac{3}{4}mg$

Conclusion:

The tensile force in each of the threads is $T = \frac{5}{4}mg$. The force of normal reaction between each load and the plank is $N = \frac{3}{4}mg$.