Question

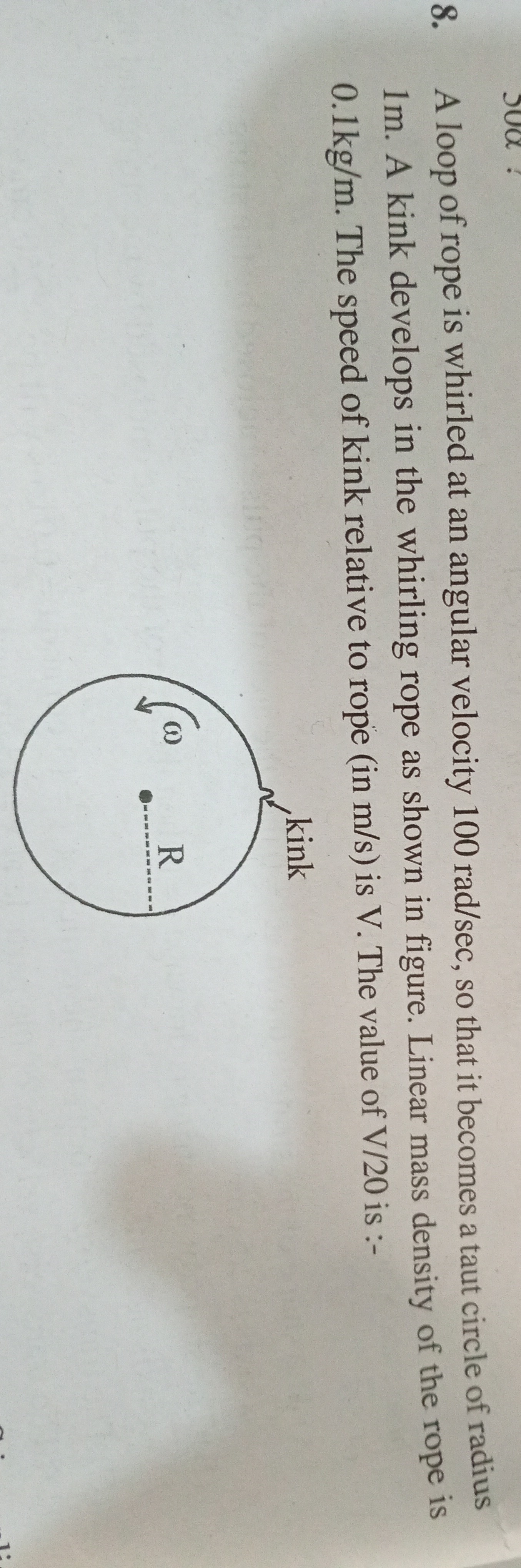
A loop of rope is whirled at an angular velocity 100 rad/sec, so that it becomes a taut circle of radius 1m. A kink develops in the whirling rope as shown in figure. Linear mass density of the rope is 0.1kg/m. The speed of kink relative to rope (in m/s) is V. The value of V/20 is :-

Answer 1

5

Answer 2

The tension in the whirling rope is caused by the centripetal force required for circular motion. For a small segment of the rope, the tension provides the necessary centripetal force. This tension is found to be $T = \mu R^2 \omega^2$. A kink in the rope is a transverse wave propagating along the rope. The speed of this wave relative to the rope is given by $V = \sqrt{T/\mu}$. Substituting the expression for T, we get $V = \sqrt{(\mu R^2 \omega^2)/\mu} = R\omega$. Using the given values, $V = 1 \times 100 = 100$ m/s. The required value is V/20, which is $100/20 = 5$.