Question
Question: A line from origin meets the lines $\frac{x-1}{1}=\frac{y}{2}=\frac{z+1}{2}$ and $\frac{x}{2}=\frac{...
A line from origin meets the lines 1x−1=2y=2z+1 and 2x=3y−1=1z at A and B, then length of AB is equal to 6.
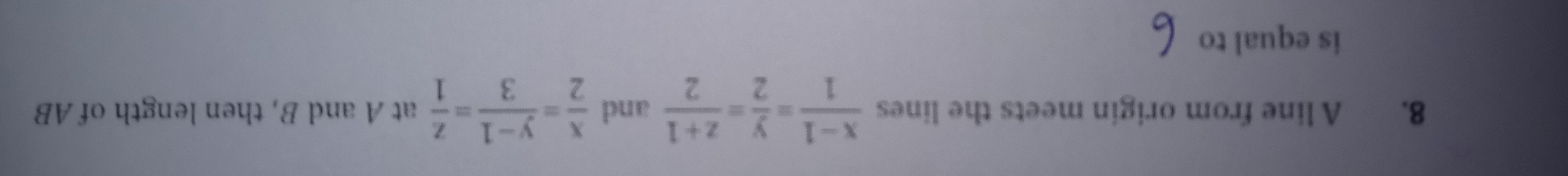
6
Solution
Let the line from the origin be L0. L0 passes through O(0,0,0). Let L1 be the line 1x−1=2y=2z+1 and L2 be the line 2x=3y−1=1z. L0 intersects L1 at point A and L2 at point B. Since A and B lie on L0, they are collinear with the origin O. Thus, the vector OA is parallel to OB.
A general point on L1 is A=(1+t1,2t1,−1+2t1) for some scalar t1. A general point on L2 is B=(2t2,1+3t2,t2) for some scalar t2.
Since O, A, and B are collinear, OA must be parallel to OB. This means the coordinates of A and B are proportional. So, (1+t1,2t1,−1+2t1)=k(2t2,1+3t2,t2) for some scalar k. This gives the system of equations:
- 1+t1=2kt2
- 2t1=k(1+3t2)
- −1+2t1=kt2
Substitute kt2 from equation (3) into equation (1): 1+t1=2(−1+2t1) 1+t1=−2+4t1 3=3t1⟹t1=1.
Now substitute t1=1 back into the equations: From (3): −1+2(1)=kt2⟹1=kt2. From (1): 1+1=2kt2⟹2=2kt2⟹kt2=1. (Consistent) From (2): 2(1)=k(1+3t2)⟹2=k+3kt2. Substitute kt2=1 into this equation: 2=k+3(1)⟹2=k+3⟹k=−1.
Now we have k=−1 and kt2=1. (−1)t2=1⟹t2=−1.
Using t1=1, the coordinates of point A are: A=(1+1,2(1),−1+2(1))=(2,2,1).
Using t2=−1, the coordinates of point B are: B=(2(−1),1+3(−1),−1)=(−2,1−3,−1)=(−2,−2,−1).
The length of the segment AB is the distance between points A and B: AB=(−2−2)2+(−2−2)2+(−1−1)2 AB=(−4)2+(−4)2+(−2)2 AB=16+16+4 AB=36 AB=6.
The problem statement asserts that "A line from origin meets the lines ... at A and B, then length of AB is equal to 6." Our calculation confirms this statement by finding the points A and B and verifying that the distance between them is indeed 6.
