Question

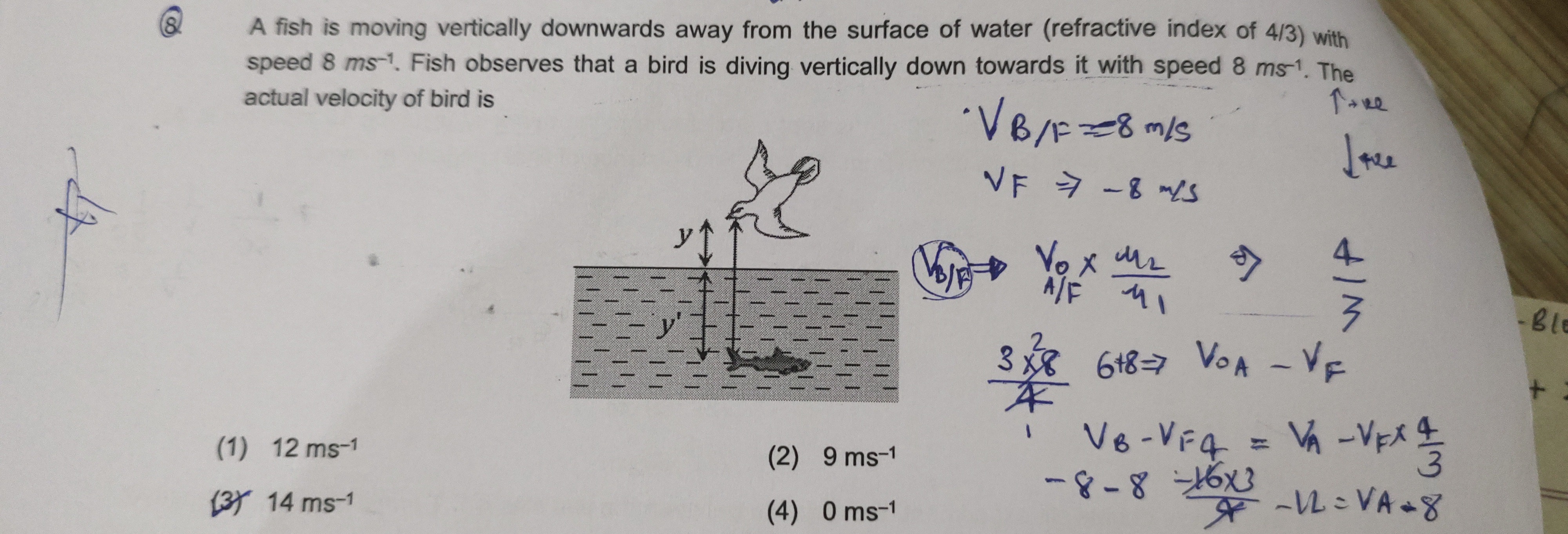
A fish is moving vertically downwards away from the surface of water (refractive index of 4/3) with speed 8 $ms^{-1}$. Fish observes that a bird is diving vertically down towards it with speed 8 $ms^{-1}$. The actual velocity of bird is

• A. 12 $ms^{-1}$
• B. 9 $ms^{-1}$
• C. 14 $ms^{-1}$
• D. 0 $ms^{-1}$

Answer 1

Answer: (C)

14 $ms^{-1}$

Answer 2

Let the upward direction be positive. The actual velocity of the fish is $v_F = -8$ m/s. The apparent relative velocity of the bird as observed by the fish is $v_{B/F, app} = -8$ m/s. The refractive index of water is $\mu_w = 4/3$, and the refractive index of air is $\mu_a = 1$.

The apparent relative velocity of an object in medium 1 observed by an observer in medium 2 is given by: $v_{obj/obs, app} = \frac{\mu_{obj}}{\mu_{obs}} v_{obj/obs, actual}$

Here, the object is the bird (in air, $\mu_a = 1$) and the observer is the fish (in water, $\mu_w = 4/3$). So, $v_{B/F, app} = \frac{\mu_a}{\mu_w} (v_B - v_F)$.

Substituting the values: $-8 = \frac{1}{4/3} (v_B - (-8))$ $-8 = \frac{3}{4} (v_B + 8)$ $-8 \times \frac{4}{3} = v_B + 8$ $-\frac{32}{3} = v_B + 8$ $v_B = -\frac{32}{3} - 8 = -\frac{32+24}{3} = -\frac{56}{3}$ m/s.

However, the solution snippet uses the formula $V_{B/F, app} = V_{B/F, actual} \times \frac{\mu_{observer}}{\mu_{object}}$. Using this formula: $v_{B/F, app} = (v_B - v_F) \times \frac{\mu_w}{\mu_a}$ $-8 = (v_B - (-8)) \times \frac{4/3}{1}$ $-8 = (v_B + 8) \times \frac{4}{3}$ $-8 \times \frac{3}{4} = v_B + 8$ $-6 = v_B + 8$ $v_B = -14$ m/s. The speed is $|v_B| = 14$ m/s.