Question

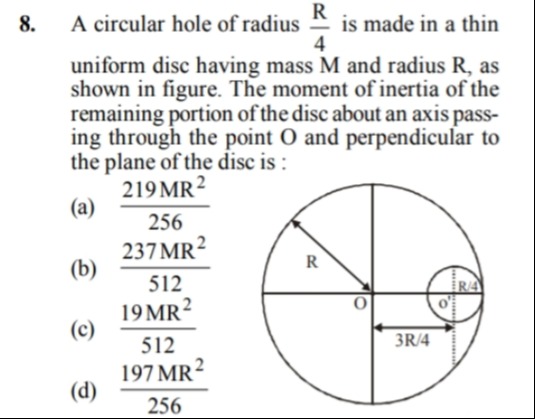
A circular hole of radius $\frac{R}{4}$ is made in a thin uniform disc having mass M and radius R, as shown in figure. The moment of inertia of the remaining portion of the disc about an axis passing through the point O and perpendicular to the plane of the disc is :

• A. $\frac{219MR^2}{256}$
• B. $\frac{237MR^2}{512}$
• C. $\frac{19MR^2}{512}$
• D. $\frac{197MR^2}{256}$

Answer 1

Answer: (B)

$\frac{237MR^2}{512}$

Answer 2

The moment of inertia of the original uniform disc of mass M and radius R about an axis passing through its center O and perpendicular to its plane is $I_{original} = \frac{1}{2}MR^2$. The disc has a uniform surface mass density $\sigma = \frac{M}{\pi R^2}$. A circular hole of radius $r = \frac{R}{4}$ is made. The mass of the removed portion (hole) is $m_{hole} = \sigma \times (\pi r^2) = \frac{M}{\pi R^2} \times \pi \left(\frac{R}{4}\right)^2 = \frac{M}{16}$. The center of the hole, O', is located at a distance $d = \frac{3R}{4}$ from the center O of the original disc. The moment of inertia of the hole about its own center O' is $I_{hole, O'} = \frac{1}{2}m_{hole}r^2 = \frac{1}{2} \left(\frac{M}{16}\right) \left(\frac{R}{4}\right)^2 = \frac{MR^2}{512}$. Using the parallel axis theorem, the moment of inertia of the hole about the axis passing through O is $I_{hole, O} = I_{hole, O'} + m_{hole}d^2 = \frac{MR^2}{512} + \left(\frac{M}{16}\right) \left(\frac{3R}{4}\right)^2 = \frac{MR^2}{512} + \frac{9MR^2}{256} = \frac{19MR^2}{512}$. The moment of inertia of the remaining portion of the disc is $I_{remaining} = I_{original} - I_{hole, O} = \frac{1}{2}MR^2 - \frac{19MR^2}{512} = \frac{256MR^2}{512} - \frac{19MR^2}{512} = \frac{237MR^2}{512}$.