Question

A block is resting over a rough horizontal floor. At t = 0, a time varying force starts acting on it, the force is described by equation $F = kt$, where k is a positive constant and t is in seconds. Mark the correct statement (s) for this situation.

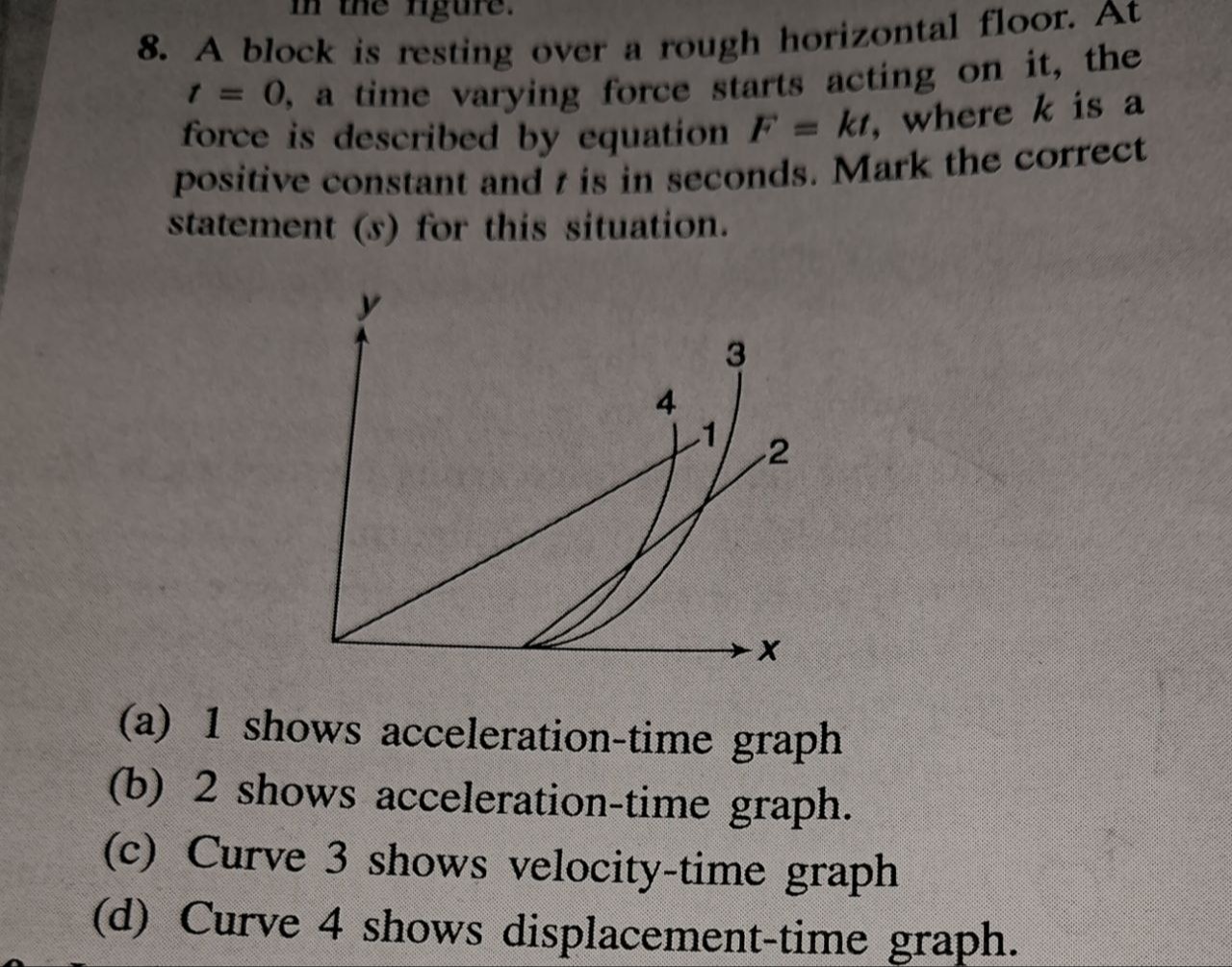
• A. 1 shows acceleration-time graph
• B. 2 shows acceleration-time graph.
• C. Curve 3 shows velocity-time graph
• D. Curve 4 shows displacement-time graph.

Answer 1

Answer: (B), (C), (D)

(b), (c), (d)

Answer 2

The problem describes a block resting on a rough horizontal floor, subjected to a time-varying force $F = kt$. We need to identify the correct graphs for acceleration, velocity, and displacement as functions of time.

Let's analyze the motion in two phases:

Phase 1: Block at rest (Static Friction)

• Initially, the block is at rest. As the force $F = kt$ increases from $t=0$, the static friction $f_s$ opposes the motion and adjusts itself to be equal to the applied force, i.e., $f_s = F = kt$.
• The block remains at rest as long as $F \le f_{s,max}$, where $f_{s,max} = \mu_s N = \mu_s mg$ (since $N=mg$ for a horizontal surface).
• Let $t_0$ be the time when the applied force equals the maximum static friction: $kt_0 = \mu_s mg \implies t_0 = \frac{\mu_s mg}{k}$.
• During this phase ($0 \le t \le t_0$):
  • Acceleration $a(t) = 0$.
  • Velocity $v(t) = 0$.
  • Displacement $x(t) = 0$.

Phase 2: Block in motion (Kinetic Friction)

• When $t > t_0$, the applied force $F = kt$ exceeds $f_{s,max}$, and the block starts to move.
• Once the block is in motion, the friction acting on it is kinetic friction, $f_k = \mu_k N = \mu_k mg$. Since typically $\mu_k < \mu_s$, $f_k < f_{s,max}$.
• The net force on the block is $F_{net} = F - f_k = kt - \mu_k mg$.
• According to Newton's second law, $F_{net} = ma$. $ma = kt - \mu_k mg$ $a(t) = \frac{k}{m}t - \mu_k g$ for $t > t_0$.

Let's analyze the graphs based on these equations:

1. Acceleration-time graph ($a$ vs $t$):

   • For $0 \le t \le t_0$, $a(t) = 0$.
   • For $t > t_0$, $a(t) = \left(\frac{k}{m}\right)t - \mu_k g$. This is a linear function of $t$ with a positive slope $\frac{k}{m}$.
   • At $t=t_0$, the acceleration jumps from $0$ to $a(t_0) = \frac{k}{m}t_0 - \mu_k g = \frac{k}{m}\left(\frac{\mu_s mg}{k}\right) - \mu_k g = (\mu_s - \mu_k)g$. Since $\mu_s > \mu_k$, $a(t_0) > 0$.
   • Curve 2 shows exactly this behavior: it's zero for an initial period, then rises linearly. So, statement (b) is correct.

2. Velocity-time graph ($v$ vs $t$):

   • For $0 \le t \le t_0$, $v(t) = 0$.
   • For $t > t_0$, $v(t) = \int a(t) dt = \int_{t_0}^{t} \left(\frac{k}{m}t' - \mu_k g\right) dt'$. $v(t) = \left[\frac{k}{2m}t'^2 - \mu_k g t'\right]_{t_0}^{t} = \left(\frac{k}{2m}t^2 - \mu_k g t\right) - \left(\frac{k}{2m}t_0^2 - \mu_k g t_0\right)$.
   • This is a quadratic function of $t$ (a parabola) for $t > t_0$. Since the coefficient of $t^2$ is $\frac{k}{2m}$ (which is positive), the parabola opens upwards (concave up).
   • Curve 3 shows this behavior: it's zero for an initial period, then increases parabolically (concave up). So, statement (c) is correct.

3. Displacement-time graph ($x$ vs $t$):

   • For $0 \le t \le t_0$, $x(t) = 0$.
   • For $t > t_0$, $x(t) = \int v(t) dt = \int_{t_0}^{t} \left(\text{quadratic function of } t'\right) dt'$.
   • Integrating a quadratic function results in a cubic function of $t$. Since velocity is always non-negative (it starts at 0 and increases), the displacement will always be non-decreasing.
   • Curve 4 shows this behavior: it's zero for an initial period, then increases very rapidly, consistent with a cubic function. So, statement (d) is correct.

4. Curve 1: This curve shows a linear increase from $t=0$. This would imply $a \propto t$ from $t=0$ if there were no static friction or if friction were negligible, which contradicts the "rough horizontal floor" condition. Thus, statement (a) is incorrect.

Therefore, statements (b), (c), and (d) are correct.