Question

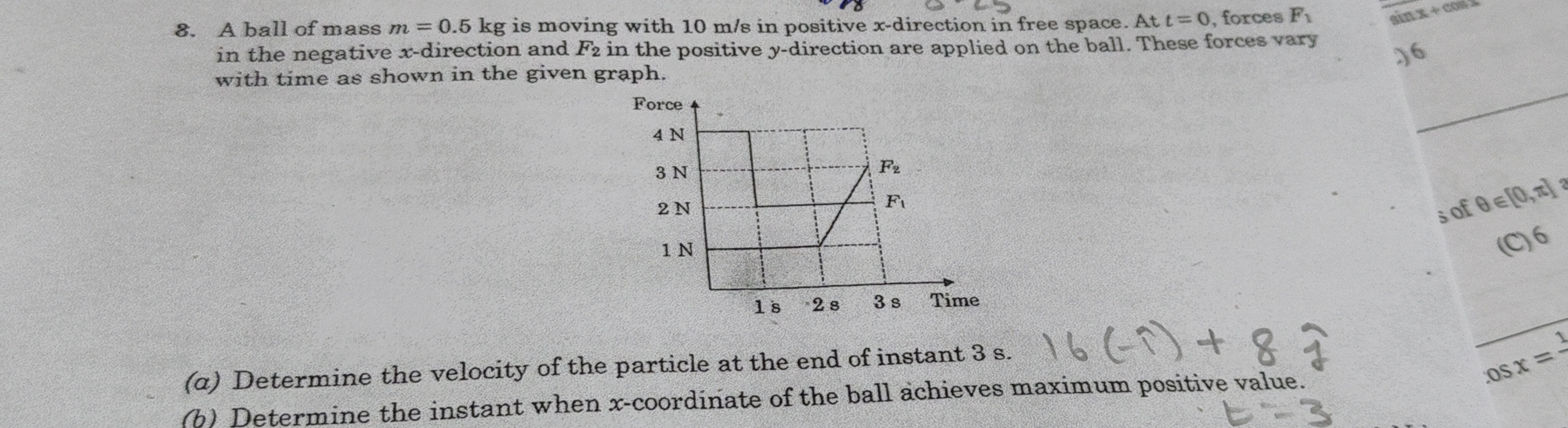
A ball of mass $m = 0.5$ kg is moving with 10 m/s in positive x-direction in free space. At $t = 0$, forces $F_1$ in the negative x-direction and $F_2$ in the positive y-direction are applied on the ball. These forces vary with time as shown in the given graph.

(a) Determine the velocity of the particle at the end of instant 3 s.

(b) Determine the instant when x-coordinate of the ball achieves maximum positive value.

Answer 1

(a) $(-1\hat{i} + 9\hat{j})$ m/s, (b) $2\sqrt{2}$ s

Answer 2

The problem involves analyzing the motion of a ball under the influence of time-varying forces using the impulse-momentum theorem.

Given:

• Mass of the ball, $m = 0.5$ kg
• Initial velocity, $\vec{v}_0 = 10 \hat{i}$ m/s (in positive x-direction).

The impulse-momentum theorem states that the change in momentum ($\Delta \vec{p}$) of an object is equal to the impulse ($\vec{J}$) applied to it:

$\Delta \vec{p} = \vec{J}$ $m(\vec{v}_f - \vec{v}_i) = \int \vec{F} dt$

This can be applied component-wise:

$m(v_{fx} - v_{ix}) = \int F_x dt$ $m(v_{fy} - v_{iy}) = \int F_y dt$

From the graph:

• Force $F_1$ acts in the negative x-direction, so $F_x = -F_1$.
• Force $F_2$ acts in the positive y-direction, so $F_y = F_2$.

Part (a): Determine the velocity of the particle at the end of instant 3 s.

1. Calculate impulse in x-direction ($J_x$):

$J_x = \int_0^3 F_x dt = -\int_0^3 F_1 dt$.

The integral $\int_0^3 F_1 dt$ is the area under the $F_1$ vs time graph from $t=0$ to $t=3$ s.

This area can be divided into three parts:

• Area from $t=0$ to $t=1$ s (rectangle): $A_1 = 1 \text{ N} \times 1 \text{ s} = 1 \text{ Ns}$.
• Area from $t=1$ to $t=2$ s (rectangle): $A_2 = 2 \text{ N} \times 1 \text{ s} = 2 \text{ Ns}$.
• Area from $t=2$ to $t=3$ s (trapezoid): $A_3 = \frac{1}{2} (2 \text{ N} + 3 \text{ N}) \times (3-2) \text{ s} = \frac{1}{2} (5 \text{ N}) \times 1 \text{ s} = 2.5 \text{ Ns}$.

Total area under $F_1$ curve = $A_1 + A_2 + A_3 = 1 + 2 + 2.5 = 5.5 \text{ Ns}$.

So, $J_x = -5.5 \text{ Ns}$.

2. Calculate final x-velocity ($v_x(3s)$):

$m(v_x(3s) - v_{0x}) = J_x$ $0.5 \text{ kg} (v_x(3s) - 10 \text{ m/s}) = -5.5 \text{ Ns}$ $v_x(3s) - 10 = -5.5 / 0.5 = -11 \text{ m/s}$ $v_x(3s) = 10 - 11 = -1 \text{ m/s}$.

3. Calculate impulse in y-direction ($J_y$):

$J_y = \int_0^3 F_y dt = \int_0^3 F_2 dt$.

The integral $\int_0^3 F_2 dt$ is the area under the $F_2$ vs time graph from $t=0$ to $t=3$ s.

This area can be divided into two parts:

• Area from $t=0$ to $t=2$ s (rectangle): $A_1 = 1 \text{ N} \times 2 \text{ s} = 2 \text{ Ns}$.
• Area from $t=2$ to $t=3$ s (trapezoid): $A_2 = \frac{1}{2} (1 \text{ N} + 4 \text{ N}) \times (3-2) \text{ s} = \frac{1}{2} (5 \text{ N}) \times 1 \text{ s} = 2.5 \text{ Ns}$.

Total area under $F_2$ curve = $A_1 + A_2 = 2 + 2.5 = 4.5 \text{ Ns}$.

So, $J_y = 4.5 \text{ Ns}$.

4. Calculate final y-velocity ($v_y(3s)$):

Initial y-velocity $v_{0y} = 0$.

$m(v_y(3s) - v_{0y}) = J_y$ $0.5 \text{ kg} (v_y(3s) - 0) = 4.5 \text{ Ns}$ $v_y(3s) = 4.5 / 0.5 = 9 \text{ m/s}$.

5. Determine the velocity vector at 3 s:

$\vec{v}(3s) = v_x(3s) \hat{i} + v_y(3s) \hat{j} = (-1 \hat{i} + 9 \hat{j}) \text{ m/s}$.

Part (b): Determine the instant when x-coordinate of the ball achieves maximum positive value.

The x-coordinate of the ball achieves its maximum positive value when its x-component of velocity ($v_x$) becomes zero. After this point, $v_x$ will become negative due to the continuous application of $F_1$ in the negative x-direction.

We set $v_x(t) = 0$:

$v_x(t) = v_{0x} + \frac{1}{m} \int_0^t F_x dt$ $0 = 10 \text{ m/s} + \frac{1}{0.5 \text{ kg}} \int_0^t (-F_1) dt$ $0 = 10 - 2 \int_0^t F_1 dt$ $2 \int_0^t F_1 dt = 10$ $\int_0^t F_1 dt = 5 \text{ Ns}$.

We need to find the time $t$ when the cumulative area under the $F_1$ vs time graph reaches $5 \text{ Ns}$.

• Area from $t=0$ to $t=1$ s: $1 \text{ Ns}$.
• Area from $t=0$ to $t=2$ s: $1 \text{ Ns} + (2 \text{ N} \times 1 \text{ s}) = 3 \text{ Ns}$.

Since $3 \text{ Ns} < 5 \text{ Ns}$, the time $t$ must be greater than $2 \text{ s}$.

Let this time be $t_m$. The additional area needed is $5 \text{ Ns} - 3 \text{ Ns} = 2 \text{ Ns}$.

This additional area must be accumulated in the interval $[2 \text{ s}, t_m]$.

In the interval $t \in [2, 3 \text{ s}]$, the force $F_1(t)$ varies linearly.

At $t=2$ s, $F_1 = 2$ N. At $t=3$ s, $F_1 = 3$ N.

The equation for the line passing through $(2,2)$ and $(3,3)$ is $F_1(t) = t$. (For $t \in [2, 3]$)

Now, we calculate the integral from $2$ to $t_m$:

$\int_2^{t_m} F_1(t) dt = 2 \text{ Ns}$ $\int_2^{t_m} t dt = 2$ $\left[ \frac{t^2}{2} \right]_2^{t_m} = 2$ $\frac{t_m^2}{2} - \frac{2^2}{2} = 2$ $\frac{t_m^2}{2} - 2 = 2$ $\frac{t_m^2}{2} = 4$ $t_m^2 = 8$ $t_m = \sqrt{8} = 2\sqrt{2} \text{ s}$.

Since $2\sqrt{2} \approx 2.828$ s, which is within the range $[2, 3]$ s, this is a valid time.