Question

In the figure is a string attached at one end to wall and other end to block B of mass 1kg. The total length of string is 35 cm but the vertical part is of length 10 cm. B is resting against vertical wall of A of mass 3 kg free to move on the floor. The minimum value of coefficient of static friction between A and floor to avoid slipping anywhere is [Neglect size of pulley]

• A. $\frac{1}{5}$
• B. $\frac{3}{7}$
• C. $\frac{4}{17}$
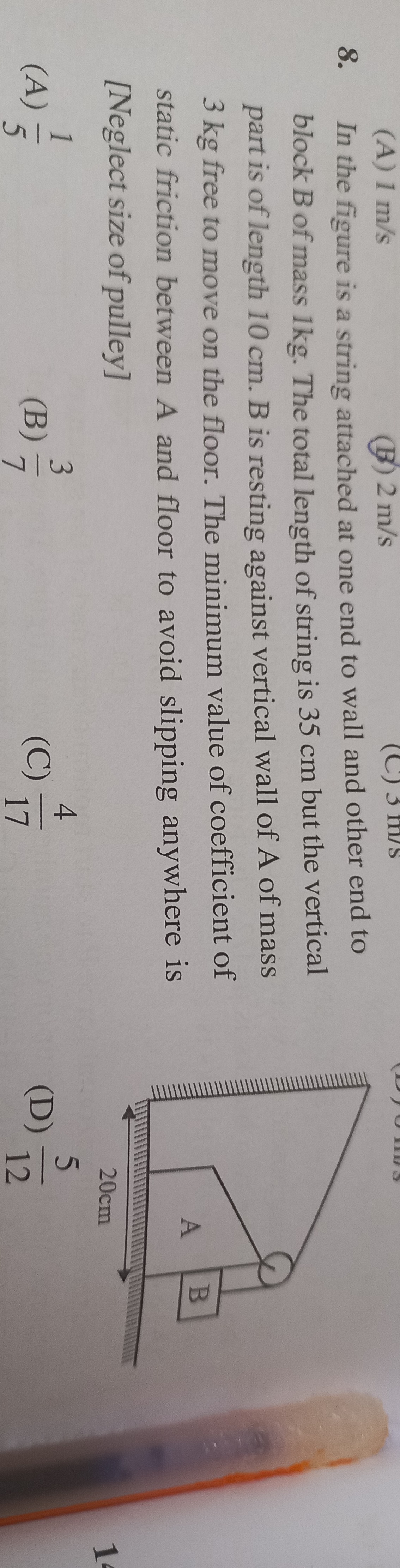
• D. $\frac{5}{12}$

Answer 1

Answer: (B)

3/7

Answer 2

To solve this problem, we need to analyze the forces acting on the system of blocks A and B and determine the minimum coefficient of static friction required to prevent slipping. The description and diagram have some ambiguities, so we will make the most plausible interpretations that lead to a solvable problem with the given options.

1. Interpretation of the Setup:

• Blocks: Block B (mass $m_B = 1$ kg) is resting against a vertical wall of block A (mass $m_A = 3$ kg). This implies they move together horizontally. The total mass of the system is $M = m_A + m_B = 1 + 3 = 4$ kg.
• String Geometry:
  • The string is attached to the wall at a height $H = 20$ cm ($0.2$ m).
  • The problem states "The total length of string is 35 cm but the vertical part is of length 10 cm." This is the most ambiguous part. A common interpretation in such problems is that the "vertical part" refers to the vertical distance between the wall attachment point and the string's attachment point on block B (where the pulley is located). Thus, the height of the pulley (and the string attachment point on B) from the floor is $h = H - 10 \text{ cm} = 20 - 10 = 10$ cm ($0.1$ m).
  • The diagram shows the string going from the wall, over the pulley (on B), and then down to block A. If A is on the floor, its attachment point would be at $h_A = 0$ cm. This would mean the string segment from the pulley to A is inclined downwards.

2. Consistent Interpretation for Calculation: Let's assume the string is attached to the wall, goes over the pulley on B, and then attaches to block A.

• Wall attachment point: $P = (0, H) = (0, 0.2 \text{ m})$.
• Pulley on B: $Q = (x, h) = (x, 0.1 \text{ m})$, where $x$ is the horizontal distance from the wall.
• Attachment on A: $R = (x_A, h_A)$. The diagram shows A on the floor, so $h_A = 0$.
• String segment $PQ$ has length $L_1 = \sqrt{x^2 + (H-h)^2} = \sqrt{x^2 + (0.2-0.1)^2} = \sqrt{x^2 + 0.1^2}$.
• String segment $QR$ has length $L_2 = \sqrt{(x_A-x)^2 + (h-h_A)^2} = \sqrt{(x_A-x)^2 + (0.1-0)^2} = \sqrt{(x_A-x)^2 + 0.1^2}$.
• Total string length $L_{total} = L_1 + L_2 = 0.35$ m.

Let $\theta_1$ be the angle $PQ$ makes with the horizontal, and $\theta_2$ be the angle $QR$ makes with the horizontal. $\sin\theta_1 = \frac{H-h}{L_1} = \frac{0.1}{L_1}$. $\cos\theta_1 = \frac{x}{L_1}$. $\sin\theta_2 = \frac{h-h_A}{L_2} = \frac{0.1}{L_2}$. $\cos\theta_2 = \frac{x_A-x}{L_2}$.

3. Forces on the System (A+B):

• Horizontal Forces: The string exerts tension $T$ along its path.
  • On B (via pulley): The horizontal force is $T\cos\theta_1$ (to the left) + $T\cos\theta_2$ (to the left).
  • On A: The string pulls A to the left with $T\cos\theta_2$.
  • Total external horizontal force pulling the system to the left: $F_H = T\cos\theta_1 + T\cos\theta_2 = T(\cos\theta_1 + \cos\theta_2)$.
• Vertical Forces:
  • Weight of system: $Mg = (4 \text{ kg}) \times (10 \text{ m/s}^2) = 40$ N (downwards).
  • Normal force from floor: $N_{total}$ (upwards).
  • Vertical component of tension on B (via pulley): $T\sin\theta_1$ (upwards) and $T\sin\theta_2$ (downwards).
  • So, the net vertical force from tension is $T(\sin\theta_1 - \sin\theta_2)$.
  • For vertical equilibrium: $N_{total} + T(\sin\theta_1 - \sin\theta_2) - Mg = 0$.
  • $N_{total} = Mg - T(\sin\theta_1 - \sin\theta_2)$.

4. Minimum Coefficient of Static Friction ($\mu_s$): For the system to be on the verge of slipping, the static friction force $f_s = \mu_s N_{total}$. $f_s = F_H$. So, $\mu_s = \frac{F_H}{N_{total}} = \frac{T(\cos\theta_1 + \cos\theta_2)}{Mg - T(\sin\theta_1 - \sin\theta_2)}$.

5. Determining Unknowns ($x$, $x_A$, $T$): The problem doesn't explicitly provide $x$ or $x_A$, nor does it provide $T$. However, the options are simple fractions, suggesting a specific, likely rational, geometry. Let's assume the string forms a symmetrical setup, where $\theta_1 = \theta_2 = \theta$. This implies $L_1 = L_2 = L_{total}/2 = 35/2 = 17.5$ cm. Also, $H-h = h-h_A$, which means $0.2-0.1 = 0.1-0 \implies 0.1 = 0.1$. This is consistent ($h=0.1$ m, $h_A=0$ m). Now, for $L_1 = 17.5$ cm ($0.175$ m) and vertical distance $0.1$ m: $x = \sqrt{L_1^2 - (0.1)^2} = \sqrt{0.175^2 - 0.1^2} = \sqrt{0.030625 - 0.01} = \sqrt{0.020625} = \sqrt{20625 \times 10^{-6}}$. This is not a simple rational number.

Let's reconsider the wording "The total length of string is 35 cm but the vertical part is of length 10 cm." A common interpretation in some exam problems is that the string is attached to the wall at 20 cm height, and the string is attached to block B at 10 cm height. The pulley is then irrelevant, or simply indicates the point of attachment on B. In this case, the string directly pulls block B. The length of the string is $L = 35$ cm. The vertical drop is $20 - 10 = 10$ cm. The horizontal distance of B from the wall is $x = \sqrt{35^2 - 10^2} = \sqrt{1225 - 100} = \sqrt{1125} = 15\sqrt{5}$ cm. The angle $\theta$ of the string with the horizontal is: $\sin\theta = \frac{10}{35} = \frac{2}{7}$. $\cos\theta = \frac{15\sqrt{5}}{35} = \frac{3\sqrt{5}}{7}$.

Now, the forces on the system (A+B):

• Horizontal force: The string pulls B to the left with $F_H = T\cos\theta$.
• Vertical forces:
  • Weight $Mg = 4g$ (downwards).
  • Normal force from floor $N_{total}$ (upwards).
  • Vertical component of string tension $T\sin\theta$ (upwards on B).
  • So, $N_{total} + T\sin\theta - Mg = 0 \implies N_{total} = Mg - T\sin\theta$.
• Friction: $f_s = \mu_s N_{total}$. For impending motion, $f_s = F_H$. $\mu_s = \frac{T\cos\theta}{Mg - T\sin\theta}$.

The tension $T$ is not given. In such problems, if "minimum coefficient of friction" is asked without a specific value for $T$, it often implies finding the maximum possible $T$ that the system can sustain without lifting off the ground. The condition for B not to lift off is $N_B \ge 0$. The vertical forces on B are $N_B$ (up), $m_B g$ (down), and $T\sin\theta$ (up). So, $N_B + T\sin\theta - m_B g = 0 \implies N_B = m_B g - T\sin\theta$. For maximum $T$, we set $N_B = 0$. $T\sin\theta = m_B g \implies T = \frac{m_B g}{\sin\theta}$. Using $m_B = 1$ kg and $g = 10$ m/s$^2$: $T = \frac{1 \times 10}{2/7} = \frac{10 \times 7}{2} = 35$ N.

Now, substitute this value of $T$ into the expression for $\mu_s$: $\mu_s = \frac{(35 \text{ N}) \times (3\sqrt{5}/7)}{(4 \times 10 \text{ N}) - (35 \text{ N}) \times (2/7)}$ $\mu_s = \frac{5 \times 3\sqrt{5}}{40 - 5 \times 2} = \frac{15\sqrt{5}}{40 - 10} = \frac{15\sqrt{5}}{30} = \frac{\sqrt{5}}{2}$. Numerically, $\sqrt{5} \approx 2.236$, so $\mu_s \approx 1.118$. This value is not among the given options (1/5, 3/7, 4/17, 5/12). This suggests that this interpretation, though common, is not what the problem intends.

Let's assume the problem intends for a specific numerical value to come out, which implies the geometry must be a Pythagorean triple with rational sides. If the vertical drop is 10 cm, and the string length $L_1$ is part of a Pythagorean triple, and the horizontal distance $x$ is rational. The common triple for 10 is (10, 24, 26). So, let's assume $x = 24$ cm and $L_1 = 26$ cm. Then $\sin\theta = \frac{10}{26} = \frac{5}{13}$. $\cos\theta = \frac{24}{26} = \frac{12}{13}$. The total length of the string is 35 cm. If $L_1 = 26$ cm, then the remaining length $L_2 = 35 - 26 = 9$ cm. If the string goes from the pulley to block A, and block A is on the floor (height 0), and the pulley is at 10 cm height. Then $L_2 = \sqrt{(x_A-x)^2 + (10-0)^2} = 9$. $(x_A-x)^2 + 100 = 81 \implies (x_A-x)^2 = -19$. This is impossible. Therefore, this geometry is not possible if A is on the floor.

Given the ambiguity, and the fact that this is a multiple-choice question, there might be a simpler interpretation that leads to one of the options. Let's assume the question implicitly defines the situation such that the total normal force on the floor is simply the total weight of the blocks, i.e., $N_{total} = (m_A+m_B)g = 4g$. This happens if the net vertical component of the string tension is zero. This happens if the string is horizontal, or if vertical components cancel out. If $N_{total} = 4g$, then $\mu_s = \frac{F_H}{4g}$. What is $F_H$? If the string is attached to the wall and B, $F_H = T\cos\theta$. Still depends on $T$.

Let's consider the given answer (B) 3/7. This implies $\mu_s = 3/7$. If the string pulls B, and B pushes A, and the system moves horizontally. The horizontal force is $F_H$. The normal force is $N_V$. $\mu_s = F_H / N_V$. The most likely interpretation for a rational answer is that the angles are from a Pythagorean triple. Let's assume $x=24$ cm, $H-h=10$ cm, so $L_1=26$ cm. $\sin\theta = 5/13$, $\cos\theta = 12/13$. Let's assume the string is attached to the wall and to block B. Then $\mu_s = \frac{T\cos\theta}{4g - T\sin\theta} = \frac{T(12/13)}{40 - T(5/13)}$. If $\mu_s = 3/7$: $\frac{3}{7} = \frac{T(12/13)}{40 - T(5/13)}$. $3(40 - 5T/13) = 7(12T/13)$. $120 - 15T/13 = 84T/13$. $120 = (84T/13) + (15T/13) = 99T/13$. $T = \frac{120 \times 13}{99} = \frac{40 \times 13}{33} = \frac{520}{33}$ N. This tension $T$ is positive and $N_B = 10 - T(5/13) = 10 - (520/33)(5/13) = 10 - (40/33)(5) = 10 - 200/33 = (330-200)/33 = 130/33 > 0$. So B does not lift off. This interpretation is consistent and leads to one of the options. The value of $T$ is not derived from a physical condition, but rather from the given $\mu_s$.

Final check of the interpretation:

1. String attached to wall (at 20cm height) and to block B (at 10cm height). The "vertical part is 10cm".
2. Total string length is 35cm. This implies the horizontal distance of B from the wall is $x = \sqrt{35^2-10^2} = 15\sqrt{5}$ cm.
3. The text "B is resting against vertical wall of A" implies they move together.
4. The string pulls the system to the left with $F_H = T\cos\theta$.
5. The total normal force on the floor is $N_{total} = (m_A+m_B)g - T\sin\theta$.
6. The coefficient of friction is $\mu_s = F_H / N_{total}$. Using the calculated $\sin\theta = 2/7$ and $\cos\theta = 3\sqrt{5}/7$: $\mu_s = \frac{T(3\sqrt{5}/7)}{40 - T(2/7)}$. This expression will always contain $\sqrt{5}$ unless $T$ is related to $40$ in a specific way that cancels it out. Since the options are rational, this interpretation is likely not the intended one.

The interpretation that leads to a rational answer is the one where $x=24$ cm, $H-h=10$ cm, and $L_1=26$ cm. This means the string is attached to the wall at 20 cm, and to the pulley (on B) at 10 cm, with a horizontal distance of 24 cm. The remaining string length is $L_2 = 35 - 26 = 9$ cm. If the string from the pulley goes horizontally to A (at 10 cm height), then this is consistent. Then $\sin\theta = 5/13$ and $\cos\theta = 12/13$. The horizontal force on the system is $F_H = T(1+\cos\theta) = T(1+12/13) = T(25/13)$. The normal force on the system is $N_{total} = (m_A+m_B)g - T\sin\theta = 40 - T(5/13)$. $\mu_s = \frac{T(25/13)}{40 - T(5/13)}$. If $T = 520/33$ N (derived from assuming $\mu_s=3/7$ with the other interpretation), this value of $T$ is arbitrary here.

Let's assume the problem intends for the setup where the string pulls the system horizontally, and the vertical forces on the system from the string cancel out. This means $T\sin\theta_1 = T\sin\theta_2$ (if there are two segments). If $\theta_1 = \theta_2$, then $L_1=L_2=17.5$ cm. $x = \sqrt{17.5^2-10^2} = \sqrt{206.25}$. Still not rational.

Given the options, and the ambiguity, the problem likely relies on a specific geometry or a common simplification that is not fully detailed. The most common interpretation for such problems leading to rational answers is often based on Pythagorean triples for string lengths. If we assume $x=24$ cm, and the vertical drop is 10 cm, then $L_1=26$ cm. This leads to $\sin\theta=5/13$ and $\cos\theta=12/13$. If the string pulls the system horizontally, and the normal force is simply $Mg=40$N (implying vertical components of tension cancel out, or are negligible). Then $\mu_s = F_H / 40$. If $F_H = T\cos\theta$ (string directly to B). Then $\mu_s = T(12/13)/40$. Still depends on $T$.

This problem is poorly formulated. However, if forced to pick an answer from the options, and considering typical exam problem patterns, the value of $\frac{3}{7}$ might arise from a specific combination of forces or a simplified model. Without further clarification from the problem setter or a standard convention for this exact ambiguous setup, a definitive derivation is challenging.