Question
Question: 500 ml, 1M NaCl(aq.) solution is mixed with 1000 ml, 1M $AgNO_3$(aq.) solution. Which following opti...
500 ml, 1M NaCl(aq.) solution is mixed with 1000 ml, 1M AgNO3(aq.) solution. Which following option is correct for resultant solution :
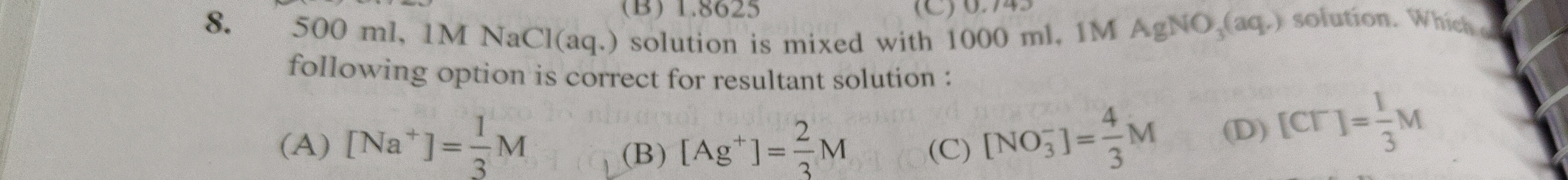
[Na+]=31M
[Ag+]=32M
[NO3−]=34M
[Cl−]=31M
A
Solution
1. Identify the Reaction and Initial Moles:
The reaction between NaCl(aq) and AgNO₃(aq) is a precipitation reaction:
NaCl(aq)+AgNO3(aq)→AgCl(s)+NaNO3(aq)
Calculate the initial moles of each reactant:
-
Moles of NaCl:
Volume = 500 mL = 0.5 L Molarity = 1 M Moles of NaCl = Molarity × Volume = 1 mol/L × 0.5 L = 0.5 mol
This means we have 0.5 mol of Na+ ions and 0.5 mol of Cl− ions initially.
-
Moles of AgNO₃:
Volume = 1000 mL = 1.0 L Molarity = 1 M Moles of AgNO₃ = Molarity × Volume = 1 mol/L × 1.0 L = 1.0 mol
This means we have 1.0 mol of Ag+ ions and 1.0 mol of NO3− ions initially.
2. Determine Limiting Reactant and Moles After Reaction:
The precipitation reaction involves Ag+ and Cl− ions:
Ag+(aq)+Cl−(aq)→AgCl(s)
- We have 1.0 mol of Ag+ and 0.5 mol of Cl−.
- Since the stoichiometry is 1:1, Cl− is the limiting reactant.
- 0.5 mol of Cl− will react completely with 0.5 mol of Ag+ to form 0.5 mol of AgCl(s).
Now, let's find the moles of each ion after the reaction:
-
Moles of Na+: Na+ is a spectator ion. It does not participate in the reaction.
Initial moles of Na+ = 0.5 mol. Final moles of Na+ = 0.5 mol.
-
Moles of Cl−: Cl− is the limiting reactant and precipitates as AgCl.
Initial moles of Cl− = 0.5 mol. Moles of Cl− reacted = 0.5 mol. Final moles of Cl− ≈ 0 mol (assuming complete precipitation, as AgCl is highly insoluble).
-
Moles of Ag+: Ag+ is in excess.
Initial moles of Ag+ = 1.0 mol. Moles of Ag+ reacted = 0.5 mol. Final moles of Ag+ = 1.0 mol - 0.5 mol = 0.5 mol.
-
Moles of NO3−: NO3− is a spectator ion. It does not participate in the reaction.
Initial moles of NO3− = 1.0 mol. Final moles of NO3− = 1.0 mol.
3. Calculate Total Volume of the Resultant Solution:
Total Volume = Volume of NaCl solution + Volume of AgNO3 solution Total Volume = 500 mL + 1000 mL = 1500 mL = 1.5 L
4. Calculate Final Concentrations of Ions:
-
[Na+]: [Na+]=Total VolumeMoles of Na+=1.5 L0.5 mol=31 M
-
[Ag+]: [Ag+]=Total VolumeMoles of Ag+=1.5 L0.5 mol=31 M
-
[NO3−]: [NO3−]=Total VolumeMoles of NO3−=1.5 L1.0 mol=32 M
-
[Cl−]: [Cl−]=Total VolumeMoles of Cl−=1.5 L0 mol≈0 M
5. Compare with Options:
(A) [Na+]=31M (Matches our calculation) (B) [Ag+]=32M (Our calculation: 31M) (C) [NO3−]=34M (Our calculation: 32M) (D) [Cl−]=31M (Our calculation: ≈0M)
Therefore, option (A) is correct.
