Question

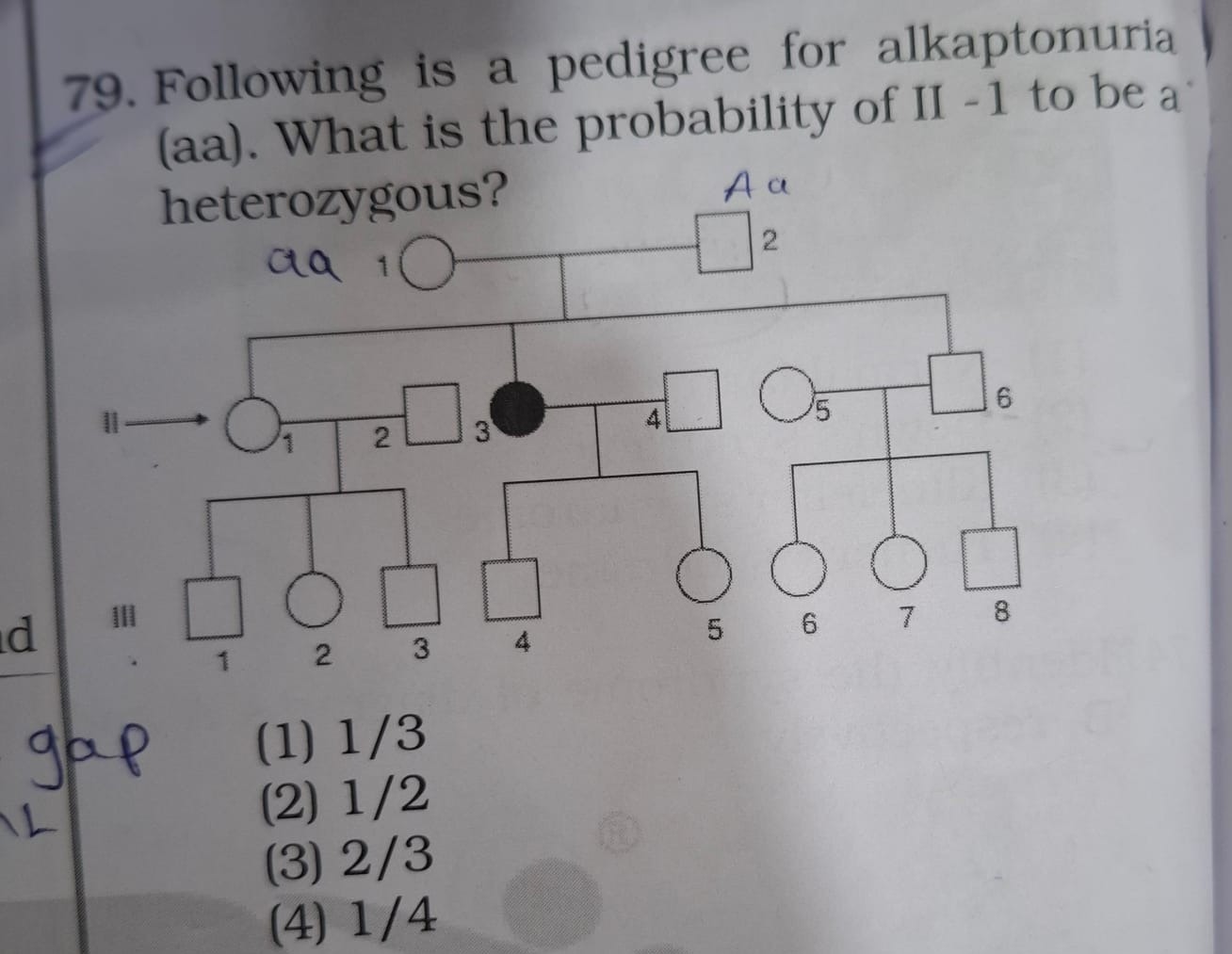
Following is a pedigree for alkaptonuria (aa). What is the probability of II -1 to be a heterozygous?

• A. 1/3
• B. 1/2
• C. 2/3
• D. 1/4

Answer 1

Answer: (C)

2/3

Answer 2

1. Identify the inheritance pattern: Alkaptonuria is a recessive genetic disorder, meaning individuals with the genotype 'aa' are affected, while individuals with at least one dominant allele 'A' (genotypes 'AA' or 'Aa') are unaffected.
2. Analyze individual II-1: Individual II-1 is an unaffected female.
3. Analyze the parents of II-1: Individual II-1 is a child of the first couple in Generation I. Let's call them I-1 (male) and I-2 (female). Both I-1 and I-2 are unaffected.
4. Interpret the label "aa" near Generation I: The notation "aa" written in blue ink near the first couple of Generation I is interpreted as an implication that this couple are both heterozygous carriers for the recessive trait. Thus, their genotype is assumed to be 'Aa' x 'Aa'.
5. Calculate probabilities for offspring of 'Aa' x 'Aa' parents: For a cross between two heterozygous individuals ('Aa' x 'Aa'), the expected genotypic ratio of their offspring is 1 AA : 2 Aa : 1 aa.
   • Probability of AA = 1/4
   • Probability of Aa = 1/2
   • Probability of aa = 1/4
6. Consider II-1's phenotype: Individual II-1 is unaffected. This means her genotype cannot be 'aa'. Her possible genotypes are 'AA' or 'Aa'.
7. Calculate the conditional probability: We need to find the probability that II-1 is heterozygous ('Aa') given that she is unaffected.
   • $P(\text{II-1 is Aa} | \text{II-1 is unaffected}) = \frac{P(\text{II-1 is Aa AND II-1 is unaffected})}{P(\text{II-1 is unaffected})}$
   • Since 'Aa' is an unaffected genotype, $P(\text{II-1 is Aa AND II-1 is unaffected}) = P(\text{II-1 is Aa}) = 1/2$.
   • $P(\text{II-1 is unaffected}) = P(AA) + P(Aa) = 1/4 + 1/2 = 3/4$.
   • Therefore, $P(\text{II-1 is Aa} | \text{II-1 is unaffected}) = \frac{1/2}{3/4} = \frac{1}{2} \times \frac{4}{3} = \frac{2}{3}$.