Question

A horizontally oriented tube AB of length $l$ rotates with a constant angular velocity $\omega$ about a stationary vertical axis OO' passing through the end A. The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.

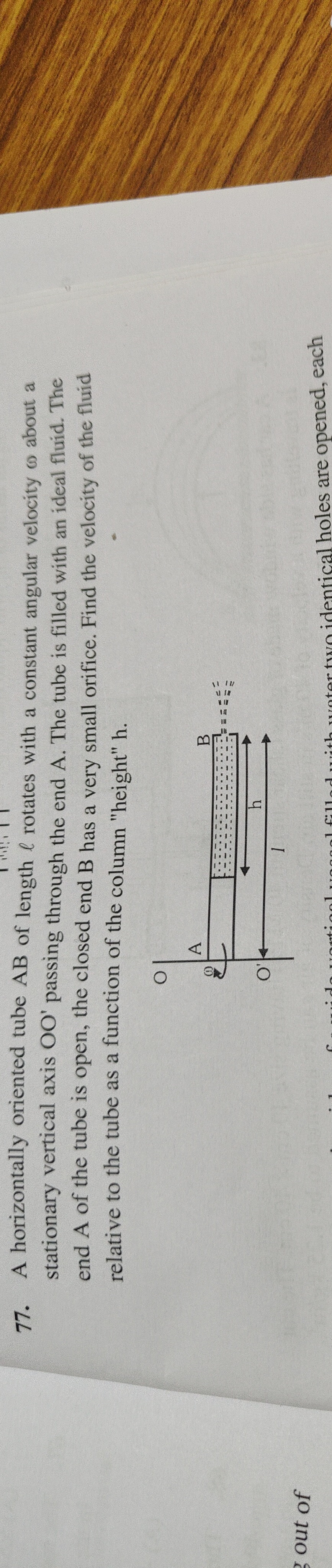
• A. v = \omega \sqrt{h(2l-h)}
• B. v = \omega \sqrt{2lh}
• C. v = \omega \sqrt{l^2 - h^2}
• D. v = \omega h

Answer 1

Answer: (A)

v = \omega \sqrt{h(2l-h)}

Answer 2

We apply Bernoulli's equation in the rotating frame. Let $x$ be the radial distance from the axis of rotation A. The Bernoulli equation is $P(x) + \frac{1}{2} \rho v(x)^2 - \frac{1}{2} \rho \omega^2 x^2 = C$. At the free surface ($x = l-h$), $P_{atm}$, $v \approx 0$. At the orifice ($x=l$), $P_{atm}$, $v$. $P_{atm} - \frac{1}{2} \rho \omega^2 (l-h)^2 = P_{atm} + \frac{1}{2} \rho v^2 - \frac{1}{2} \rho \omega^2 l^2$ $\frac{1}{2} \rho v^2 = \frac{1}{2} \rho \omega^2 (l^2 - (l-h)^2)$ $v^2 = \omega^2 (l^2 - (l^2 - 2lh + h^2)) = \omega^2 (2lh - h^2)$ $v = \omega \sqrt{h(2l-h)}$