Solveeit Logo
Login

Question

Question: If $(1 + x + x^2 + ... + x^9)^4 (x + x^2 + x^3 + ... + x^9)$ $\displaystyle = \sum_{r=1}^{45} a_r x^...

If (1+x+x2+...+x9)4(x+x2+x3+...+x9)(1 + x + x^2 + ... + x^9)^4 (x + x^2 + x^3 + ... + x^9) =∑r=145arxr\displaystyle = \sum_{r=1}^{45} a_r x^r and the value of a2+a6+a10+...+a42a_2 + a_6 + a_{10} + ... + a_{42} is λ\lambda, the sum of all digits of λ\lambda is

Answer

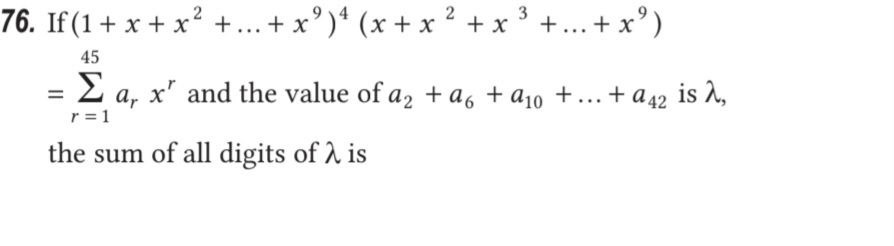
9

Explanation

Solution

To find the sum of coefficients a2+a6+a10+...+a42a_2 + a_6 + a_{10} + ... + a_{42}, we use the property of roots of unity. Let the given expression be P(x)P(x). P(x)=(1+x+x2+...+x9)4(x+x2+x3+...+x9)P(x) = (1 + x + x^2 + ... + x^9)^4 (x + x^2 + x^3 + ... + x^9)

Let S(x)=1+x+x2+...+x9S(x) = 1 + x + x^2 + ... + x^9. This is a geometric series sum: S(x)=x10−1x−1S(x) = \frac{x^{10}-1}{x-1}. The second term is x+x2+...+x9=x(1+x+...+x8)x + x^2 + ... + x^9 = x(1 + x + ... + x^8). Notice that x+x2+...+x9=(1+x+...+x9)−1=S(x)−1x + x^2 + ... + x^9 = (1 + x + ... + x^9) - 1 = S(x) - 1. So, P(x)=(S(x))4(S(x)−1)P(x) = (S(x))^4 (S(x)-1).

We are given P(x)=∑r=145arxrP(x) = \sum_{r=1}^{45} a_r x^r. We need to find λ=a2+a6+a10+...+a42\lambda = a_2 + a_6 + a_{10} + ... + a_{42}. The indices are of the form 4k+24k+2. This means we need the sum of coefficients ara_r where r≡2(mod4)r \equiv 2 \pmod 4.

For a polynomial Q(x)=∑r=0NarxrQ(x) = \sum_{r=0}^N a_r x^r, the sum of coefficients ak+ak+m+ak+2m+...a_k + a_{k+m} + a_{k+2m} + ... is given by the formula: 1m∑j=0m−1ω−kjQ(ωj)\frac{1}{m} \sum_{j=0}^{m-1} \omega^{-kj} Q(\omega^j), where ω=e2πi/m\omega = e^{2\pi i/m}. In our case, Q(x)=P(x)Q(x) = P(x), m=4m=4, and k=2k=2. So, λ=14[ω−2⋅0P(ω0)+ω−2⋅1P(ω1)+ω−2⋅2P(ω2)+ω−2⋅3P(ω3)]\lambda = \frac{1}{4} [ \omega^{-2 \cdot 0} P(\omega^0) + \omega^{-2 \cdot 1} P(\omega^1) + \omega^{-2 \cdot 2} P(\omega^2) + \omega^{-2 \cdot 3} P(\omega^3) ]. Here ω=e2πi/4=i\omega = e^{2\pi i/4} = i. λ=14[P(1)+i−2P(i)+i−4P(i2)+i−6P(i3)]\lambda = \frac{1}{4} [ P(1) + i^{-2} P(i) + i^{-4} P(i^2) + i^{-6} P(i^3) ] Since i2=−1i^2 = -1, i4=1i^4 = 1, i6=−1i^6 = -1: λ=14[P(1)−P(i)+P(−1)−P(−i)]\lambda = \frac{1}{4} [ P(1) - P(i) + P(-1) - P(-i) ].

Now, we need to evaluate S(x)S(x) at x=1,−1,i,−ix=1, -1, i, -i.

  1. S(1)=1+1+...+1S(1) = 1 + 1 + ... + 1 (10 terms) =10= 10.

  2. S(−1)=1−1+1−1+...+1−1S(-1) = 1 - 1 + 1 - 1 + ... + 1 - 1 (10 terms) =0= 0.

  3. S(i)=i10−1i−1=(i4)2i2−1i−1=12(−1)−1i−1=−2i−1S(i) = \frac{i^{10}-1}{i-1} = \frac{(i^4)^2 i^2 - 1}{i-1} = \frac{1^2(-1)-1}{i-1} = \frac{-2}{i-1}. To simplify: −2i−1×i+1i+1=−2(i+1)i2−1=−2(i+1)−1−1=−2(i+1)−2=i+1\frac{-2}{i-1} \times \frac{i+1}{i+1} = \frac{-2(i+1)}{i^2-1} = \frac{-2(i+1)}{-1-1} = \frac{-2(i+1)}{-2} = i+1.

  4. S(−i)=(−i)10−1−i−1=i10−1−i−1=−1−1−i−1=−2−(i+1)=2i+1S(-i) = \frac{(-i)^{10}-1}{-i-1} = \frac{i^{10}-1}{-i-1} = \frac{-1-1}{-i-1} = \frac{-2}{-(i+1)} = \frac{2}{i+1}. To simplify: 2i+1×1−i1−i=2(1−i)1−i2=2(1−i)1−(−1)=2(1−i)2=1−i\frac{2}{i+1} \times \frac{1-i}{1-i} = \frac{2(1-i)}{1-i^2} = \frac{2(1-i)}{1-(-1)} = \frac{2(1-i)}{2} = 1-i.

Next, evaluate P(x)=(S(x))4(S(x)−1)P(x) = (S(x))^4 (S(x)-1) at x=1,−1,i,−ix=1, -1, i, -i.

  1. P(1)=(S(1))4(S(1)−1)=(10)4(10−1)=10000×9=90000P(1) = (S(1))^4 (S(1)-1) = (10)^4 (10-1) = 10000 \times 9 = 90000.

  2. P(−1)=(S(−1))4(S(−1)−1)=(0)4(0−1)=0P(-1) = (S(-1))^4 (S(-1)-1) = (0)^4 (0-1) = 0.

  3. P(i)=(S(i))4(S(i)−1)=(i+1)4(i+1−1)=(i+1)4(i)P(i) = (S(i))^4 (S(i)-1) = (i+1)^4 (i+1-1) = (i+1)^4 (i). We know (i+1)2=i2+2i+1=−1+2i+1=2i(i+1)^2 = i^2+2i+1 = -1+2i+1 = 2i. So (i+1)4=(2i)2=4i2=−4(i+1)^4 = (2i)^2 = 4i^2 = -4. Therefore, P(i)=(−4)(i)=−4iP(i) = (-4)(i) = -4i.

  4. P(−i)=(S(−i))4(S(−i)−1)=(1−i)4(1−i−1)=(1−i)4(−i)P(-i) = (S(-i))^4 (S(-i)-1) = (1-i)^4 (1-i-1) = (1-i)^4 (-i). We know (1−i)2=1−2i+i2=1−2i−1=−2i(1-i)^2 = 1-2i+i^2 = 1-2i-1 = -2i. So (1−i)4=(−2i)2=4i2=−4(1-i)^4 = (-2i)^2 = 4i^2 = -4. Therefore, P(−i)=(−4)(−i)=4iP(-i) = (-4)(-i) = 4i.

Finally, substitute these values into the formula for λ\lambda: λ=14[P(1)−P(i)+P(−1)−P(−i)]\lambda = \frac{1}{4} [ P(1) - P(i) + P(-1) - P(-i) ] λ=14[90000−(−4i)+0−(4i)]\lambda = \frac{1}{4} [ 90000 - (-4i) + 0 - (4i) ] λ=14[90000+4i−4i]\lambda = \frac{1}{4} [ 90000 + 4i - 4i ] λ=14[90000]\lambda = \frac{1}{4} [ 90000 ] λ=22500\lambda = 22500.

The question asks for the sum of all digits of λ\lambda. Sum of digits of λ=2+2+5+0+0=9\lambda = 2+2+5+0+0 = 9.

The final answer is 9\boxed{9}.