Question

$n$ moles of He gas is placed in a vessel of volume $V$ L at $T$ K. If $V_1$ is free volume of He, then the diameter of He atom is

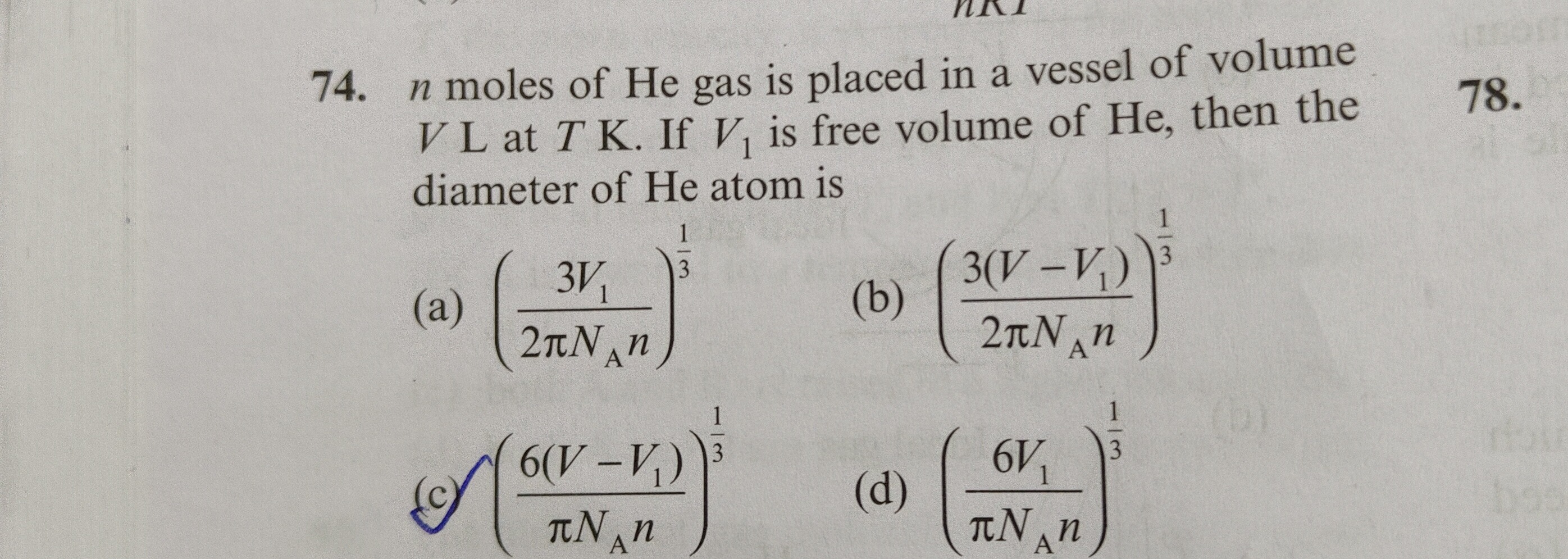
• A. (a) $\left(\frac{3V_1}{2\pi N_A n}\right)^{\frac{1}{3}}$
• B. (b) $\left(\frac{3(V-V_1)}{2\pi N_A n}\right)^{\frac{1}{3}}$
• C. (c) $\left(\frac{6(V-V_1)}{\pi N_A n}\right)^{\frac{1}{3}}$
• D. (d) $\left(\frac{6V_1}{\pi N_A n}\right)^{\frac{1}{3}}$

Answer 1

Answer: (C)

(c) $\left(\frac{6(V-V_1)}{\pi N_A n}\right)^{\frac{1}{3}}$

Answer 2

The volume occupied by $n$ moles of He atoms is $V - V_1$. This volume equals $n N_A v_{atom}$, where $v_{atom}$ is the volume of a single atom. Thus, $v_{atom} = \frac{V - V_1}{n N_A}$. Assuming the atom is a sphere with radius $r$, $v_{atom} = \frac{4}{3}\pi r^3$. Equating these, $\frac{4}{3}\pi r^3 = \frac{V - V_1}{n N_A}$. Solving for the diameter $d = 2r$, we get $d = \left(\frac{6(V - V_1)}{\pi n N_A}\right)^{1/3}$.