Question

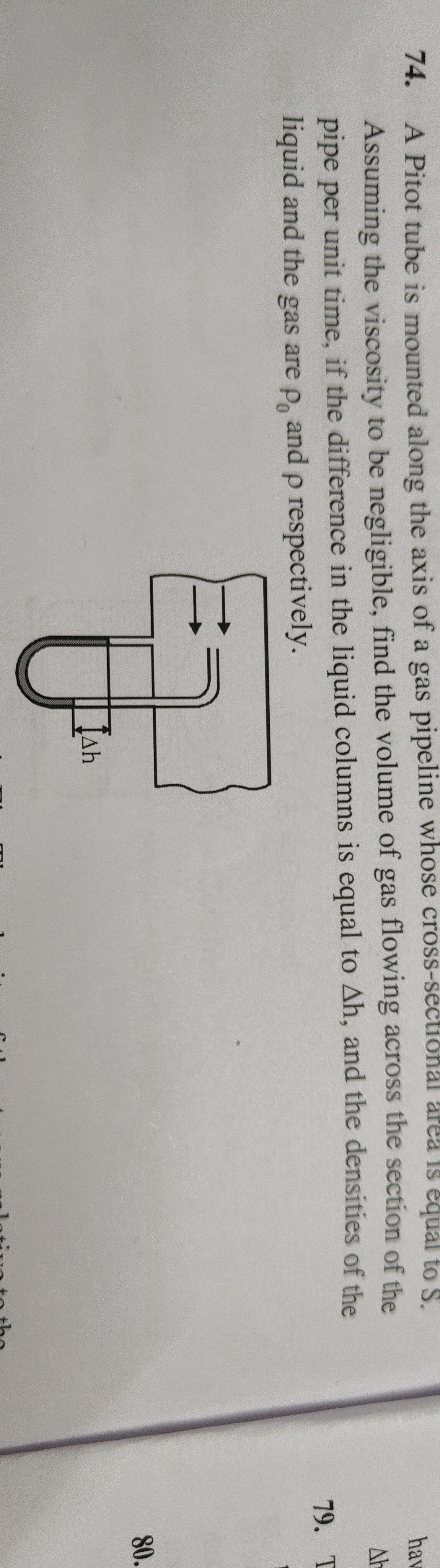
A Pitot tube is mounted along the axis of a gas pipeline whose cross-sectional area is equal to S. Assuming the viscosity to be negligible, find the volume of gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to $\Delta h$, and the densities of the liquid and the gas are $\rho_0$ and $\rho$ respectively.

Answer 1

Q = S \sqrt{\frac{2 \rho_0 g \Delta h}{\rho}}

Answer 2

The pressure difference measured by the manometer is $\rho_0 g \Delta h$. According to Bernoulli's principle, this pressure difference equals the dynamic pressure of the gas flow, which is $\frac{1}{2} \rho v^2$. Equating these, we get $\rho_0 g \Delta h = \frac{1}{2} \rho v^2$. Solving for the gas velocity $v$ gives $v = \sqrt{\frac{2 \rho_0 g \Delta h}{\rho}}$. The volume flow rate $Q$ is the product of the cross-sectional area $S$ and the velocity $v$, so $Q = S v = S \sqrt{\frac{2 \rho_0 g \Delta h}{\rho}}$.