Question

The equation $2x^3 - 3x^2 + p = 0$ has 3 distinct real roots then the value of $[p]$ is (Where [.] denotes the greatest integer function).

Answer 1

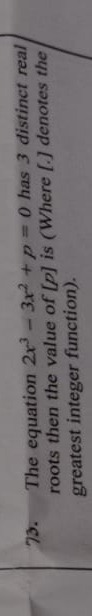
0

Answer 2

To determine the value of $[p]$ such that the equation $2x^3 - 3x^2 + p = 0$ has 3 distinct real roots, we will use the concept of local maxima and minima of a polynomial function.

Let $f(x) = 2x^3 - 3x^2 + p$. For a cubic equation to have 3 distinct real roots, its local maximum and local minimum values must have opposite signs.

Step 1: Find the critical points. First, find the derivative of $f(x)$: $f'(x) = \frac{d}{dx}(2x^3 - 3x^2 + p) = 6x^2 - 6x$

Set $f'(x) = 0$ to find the critical points: $6x^2 - 6x = 0$ $6x(x - 1) = 0$ This gives us two critical points: $x = 0$ and $x = 1$.

Step 2: Determine local maxima and minima. Find the second derivative of $f(x)$: $f''(x) = \frac{d}{dx}(6x^2 - 6x) = 12x - 6$

Evaluate $f''(x)$ at the critical points:

• At $x = 0$: $f''(0) = 12(0) - 6 = -6$. Since $f''(0) < 0$, $x = 0$ is a point of local maximum. The local maximum value is $f(0) = 2(0)^3 - 3(0)^2 + p = p$.

• At $x = 1$: $f''(1) = 12(1) - 6 = 6$. Since $f''(1) > 0$, $x = 1$ is a point of local minimum. The local minimum value is $f(1) = 2(1)^3 - 3(1)^2 + p = 2 - 3 + p = p - 1$.

Step 3: Apply the condition for 3 distinct real roots. For the equation $f(x) = 0$ to have 3 distinct real roots, the local maximum value must be positive and the local minimum value must be negative. In other words, their product must be negative: $f(0) \cdot f(1) < 0$ $p \cdot (p - 1) < 0$

Step 4: Solve the inequality for p. The inequality $p(p - 1) < 0$ holds true when $p$ is strictly between the roots of $p(p-1)=0$, which are $p=0$ and $p=1$. So, the range for $p$ is $0 < p < 1$.

Step 5: Determine the value of $[p]$. The question asks for the value of $[p]$, where $[.]$ denotes the greatest integer function. Since $0 < p < 1$, the greatest integer less than or equal to $p$ is $0$. For example, if $p = 0.5$, then $[p] = [0.5] = 0$. If $p = 0.99$, then $[p] = [0.99] = 0$.

Therefore, the value of $[p]$ is $0$.