Question

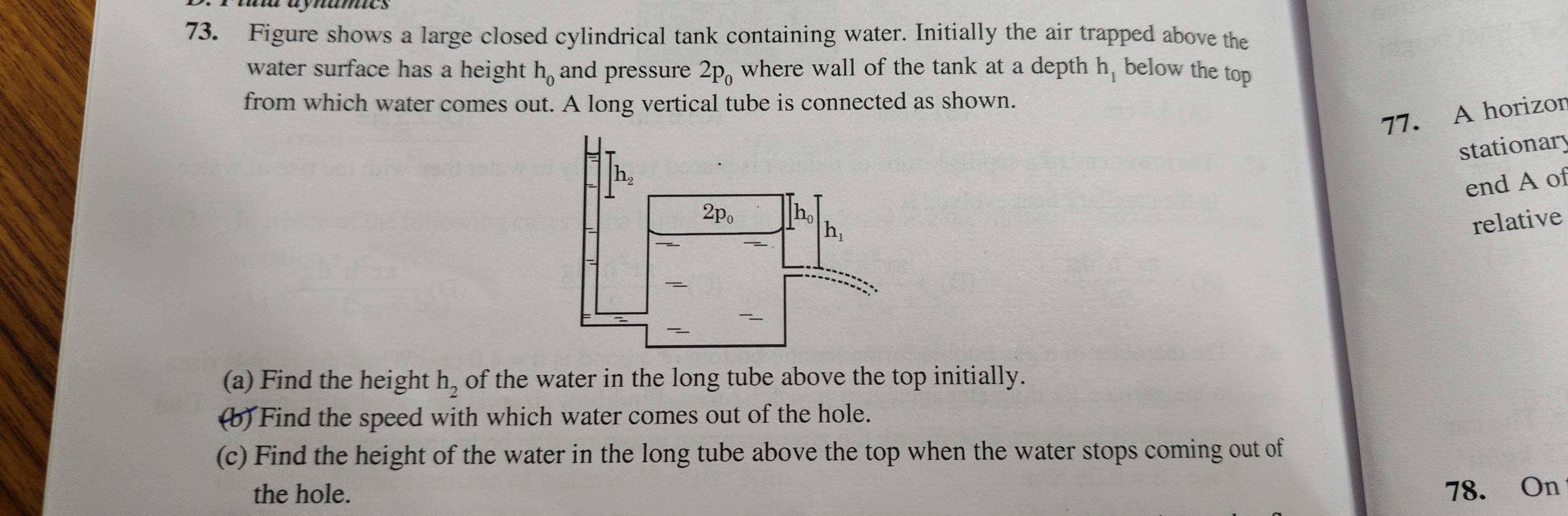
Figure shows a large closed cylindrical tank containing water. Initially the air trapped above the water surface has a height $h_0$ and pressure $2p_0$ where wall of the tank at a depth $h_1$ below the top from which water comes out. A long vertical tube is connected as shown.

(a) Find the height $h_2$ of the water in the long tube above the top initially.

(b) Find the speed with which water comes out of the hole.

(c) Find the height of the water in the long tube above the top when the water stops coming out of the hole.

Answer 1

Part (a): $h_2 = \frac{P_{atm}}{\rho g} - h_0$. Part (b): $v = \sqrt{\frac{2}{\rho} \left( P_{atm} + \rho g (h_1 - h_0) \right)}$. Part (c): $h'_2 = \frac{P_{atm}}{\rho g} \left( \frac{2h_0}{h'_0} - 1 \right) - h'_0$, where $h'_0 = \frac{h_1 + \sqrt{h_1^2 + 8 \frac{P_{atm}}{\rho g} h_0}}{2}$.

Answer 2

Part (a): Assume the top of the tank is at $z=0$. The initial air pressure is $P_{air,i} = 2p_0 = 2P_{atm}$. The air occupies the region from $z_w$ to $z_w+h_0$. If the top of the air column is at $z=0$, then $z_w = -h_0$. The pressure at the hole level ($z=-h_1$) inside the tank is $P_{tank, hole} = P_{air,i} + \rho g (z_w - (-h_1)) = 2P_{atm} + \rho g (-h_0 + h_1)$. In the long tube, the water level is at $z=h_2$, exposed to $P_{atm}$. The pressure at the hole level ($z=-h_1$) in the tube is $P_{tube, hole} = P_{atm} + \rho g (h_2 - (-h_1)) = P_{atm} + \rho g (h_2 + h_1)$. Equating pressures at $z=-h_1$: $2P_{atm} + \rho g (h_1 - h_0) = P_{atm} + \rho g (h_2 + h_1)$. This simplifies to $P_{atm} + \rho g (-h_0) = \rho g h_2$, so $h_2 = \frac{P_{atm}}{\rho g} - h_0$.

Part (b): Using Bernoulli's equation between the water surface (point 1) and the hole (point 2): $P_1 + \frac{1}{2}\rho v_1^2 + \rho g z_1 = P_2 + \frac{1}{2}\rho v_2^2 + \rho g z_2$. Here $P_1 = 2P_{atm}$, $v_1 \approx 0$, $z_1 = -h_0$. $P_2 = P_{atm}$, $v_2 = v$, $z_2 = -h_1$. So, $2P_{atm} + \rho g (-h_0) = P_{atm} + \frac{1}{2}\rho v^2 + \rho g (-h_1)$. Rearranging gives $\frac{1}{2}\rho v^2 = P_{atm} + \rho g (h_1 - h_0)$, leading to $v = \sqrt{\frac{2}{\rho} \left( P_{atm} + \rho g (h_1 - h_0) \right)}$.

Part (c): Water stops flowing when the pressure at the hole level inside the tank equals $P_{atm}$. Let the final air pressure be $P'_{air}$ and the final air height be $h'_0$. By Boyle's Law, $2P_{atm} h_0 = P'_{air} h'_0$. When flow stops, $P'_{air} + \rho g (h_1 - h'_0) = P_{atm}$. Solving for $P'_{air}$ and substituting into Boyle's law yields a quadratic equation for $h'_0$: $(h'_0)^2 - h_1 h'_0 - 2 \frac{P_{atm}}{\rho g} h_0 = 0$. The positive solution is $h'_0 = \frac{h_1 + \sqrt{h_1^2 + 8 \frac{P_{atm}}{\rho g} h_0}}{2}$. For the long tube, assuming connection at the bottom, pressure balance gives $h'_2 = \frac{P'_{air} - P_{atm}}{\rho g} - h'_0$. Substituting $P'_{air} = \frac{2P_{atm} h_0}{h'_0}$ and $P_{atm} = P'_{air} + \rho g (h_1 - h'_0)$, we get $h'_2 = \frac{P_{atm}}{\rho g} \left( \frac{2h_0}{h'_0} - 1 \right) - h'_0$.