Solveeit Logo
Login

Question

Question: If $f(x) = \begin{vmatrix} \cos(x+\alpha) & \cos(x+\beta) & \cos(x+\gamma) \\ \sin(x+\alpha) & \sin(...

If f(x)=∣cos⁡(x+α)cos⁡(x+β)cos⁡(x+γ)sin⁡(x+α)sin⁡(x+β)sin⁡(x+γ)sin⁡(β−γ)sin⁡(γ−β)sin⁡(α−β)∣f(x) = \begin{vmatrix} \cos(x+\alpha) & \cos(x+\beta) & \cos(x+\gamma) \\ \sin(x+\alpha) & \sin(x+\beta) & \sin(x + \gamma) \\ \sin(\beta-\gamma) & \sin(\gamma-\beta) & \sin(\alpha-\beta) \end{vmatrix}

and f(0)=14f(0) = \frac{1}{4}, then [∑r=115f(xr)]\left[ \sum_{r=1}^{15} f(x_r) \right] is (where [.] is G.I.F.)

Answer

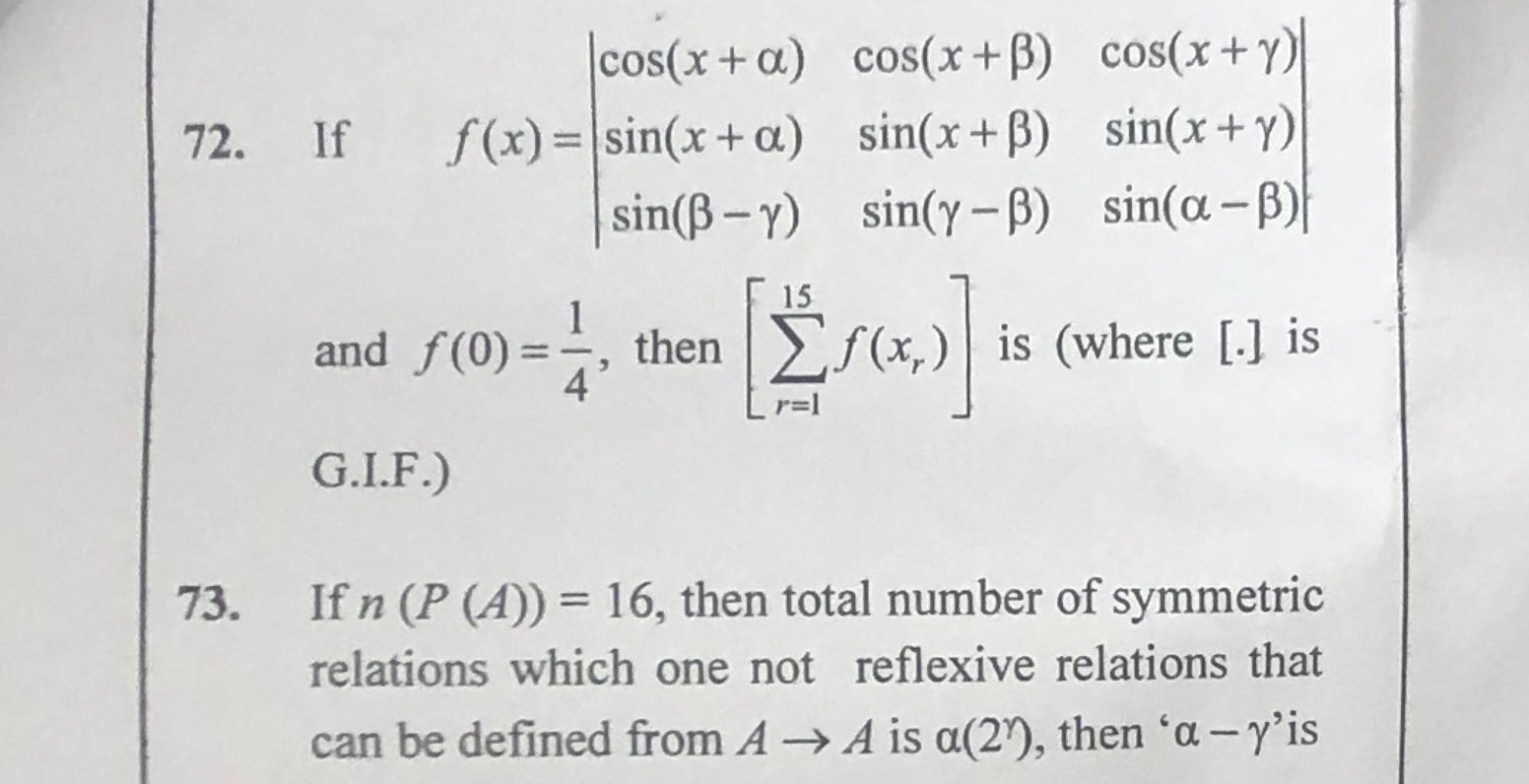
3

Explanation

Solution

The given function f(x)f(x) is a determinant. Expanding the determinant along the third row: f(x)=sin⁡(β−γ)∣cos⁡(x+β)cos⁡(x+γ)sin⁡(x+β)sin⁡(x+γ)∣−sin⁡(γ−β)∣cos⁡(x+α)cos⁡(x+γ)sin⁡(x+α)sin⁡(x+γ)∣+sin⁡(α−β)∣cos⁡(x+α)cos⁡(x+β)sin⁡(x+α)sin⁡(x+β)∣f(x) = \sin(\beta-\gamma) \begin{vmatrix} \cos(x+\beta) & \cos(x+\gamma) \\ \sin(x+\beta) & \sin(x+\gamma) \end{vmatrix} - \sin(\gamma-\beta) \begin{vmatrix} \cos(x+\alpha) & \cos(x+\gamma) \\ \sin(x+\alpha) & \sin(x+\gamma) \end{vmatrix} + \sin(\alpha-\beta) \begin{vmatrix} \cos(x+\alpha) & \cos(x+\beta) \\ \sin(x+\alpha) & \sin(x+\beta) \end{vmatrix}

Using the identity ∣cos⁡Acos⁡Bsin⁡Asin⁡B∣=cos⁡Asin⁡B−cos⁡Bsin⁡A=sin⁡(B−A)\begin{vmatrix} \cos A & \cos B \\ \sin A & \sin B \end{vmatrix} = \cos A \sin B - \cos B \sin A = \sin(B-A): The first determinant is sin⁡((x+γ)−(x+β))=sin⁡(γ−β)\sin((x+\gamma)-(x+\beta)) = \sin(\gamma-\beta). The second determinant is sin⁡((x+γ)−(x+α))=sin⁡(γ−α)\sin((x+\gamma)-(x+\alpha)) = \sin(\gamma-\alpha). The third determinant is sin⁡((x+β)−(x+α))=sin⁡(β−α)\sin((x+\beta)-(x+\alpha)) = \sin(\beta-\alpha).

So, f(x)=sin⁡(β−γ)sin⁡(γ−β)−sin⁡(γ−β)sin⁡(γ−α)+sin⁡(α−β)sin⁡(β−α)f(x) = \sin(\beta-\gamma)\sin(\gamma-\beta) - \sin(\gamma-\beta)\sin(\gamma-\alpha) + \sin(\alpha-\beta)\sin(\beta-\alpha). Since sin⁡(γ−β)=−sin⁡(β−γ)\sin(\gamma-\beta) = -\sin(\beta-\gamma) and sin⁡(β−α)=−sin⁡(α−β)\sin(\beta-\alpha) = -\sin(\alpha-\beta): f(x)=sin⁡(β−γ)(−sin⁡(β−γ))−(−sin⁡(β−γ))sin⁡(γ−α)+sin⁡(α−β)(−sin⁡(α−β))f(x) = \sin(\beta-\gamma)(-\sin(\beta-\gamma)) - (-\sin(\beta-\gamma))\sin(\gamma-\alpha) + \sin(\alpha-\beta)(-\sin(\alpha-\beta)) f(x)=−sin⁡2(β−γ)+sin⁡(β−γ)sin⁡(γ−α)−sin⁡2(α−β)f(x) = -\sin^2(\beta-\gamma) + \sin(\beta-\gamma)\sin(\gamma-\alpha) - \sin^2(\alpha-\beta).

This expression is independent of xx, meaning f(x)f(x) is a constant function. Given f(0)=14f(0) = \frac{1}{4}, we have f(x)=14f(x) = \frac{1}{4} for all xx.

We need to calculate [∑r=115f(xr)]\left[ \sum_{r=1}^{15} f(x_r) \right]. ∑r=115f(xr)=∑r=11514=15×14=154\sum_{r=1}^{15} f(x_r) = \sum_{r=1}^{15} \frac{1}{4} = 15 \times \frac{1}{4} = \frac{15}{4}. The greatest integer function of this sum is [154]=[3.75]=3\left[ \frac{15}{4} \right] = [3.75] = 3.