Question

If $\int \frac{e^x(x-1)(x-lnx)}{x^2} dx = \frac{e^x(lx+mlnx+n)}{x}+c$

(where c is integration constant and $l,m,n \in N$), then $(l-m-n)$ is equal to

Answer 1

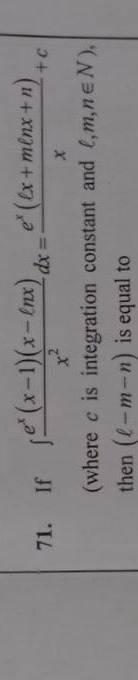
3

Answer 2

The given integral is $\int \frac{e^x(x-1)(x-lnx)}{x^2} dx$.

Expanding the numerator: $(x-1)(x-\ln x) = x^2 - x \ln x - x + \ln x$.

The integrand becomes: $\frac{e^x(x^2 - x \ln x - x + \ln x)}{x^2} = e^x \left( \frac{x^2}{x^2} - \frac{x \ln x}{x^2} - \frac{x}{x^2} + \frac{\ln x}{x^2} \right)$ $= e^x \left( 1 - \frac{\ln x}{x} - \frac{1}{x} + \frac{\ln x}{x^2} \right)$

Let's consider the structure of the result: $\frac{e^x(lx+mlnx+n)}{x}+c$. This suggests that the solution is of the form $e^x \times (\text{some function of x})$. Let the function be $f(x) = \frac{lx+mlnx+n}{x} = l + \frac{m \ln x}{x} + \frac{n}{x}$.

We need to find $F'(x)$ and match it to the integrand. $F(x) = \frac{e^x(lx+mlnx+n)}{x} = e^x \left( l + \frac{m \ln x}{x} + \frac{n}{x} \right)$. $F'(x) = e^x \left( l + \frac{m \ln x}{x} + \frac{n}{x} + m \frac{\frac{1}{x} \cdot x - \ln x \cdot 1}{x^2} + n \frac{-1}{x^2} \right)$ $F'(x) = e^x \left( l + \frac{m \ln x}{x} + \frac{n}{x} + \frac{m(1-\ln x)}{x^2} - \frac{n}{x^2} \right)$ $F'(x) = e^x \left( l + \frac{m \ln x}{x} + \frac{n}{x} + \frac{m}{x^2} - \frac{m \ln x}{x^2} - \frac{n}{x^2} \right)$

Now, equate this to the original integrand: $e^x \left( 1 - \frac{\ln x}{x} - \frac{1}{x} + \frac{\ln x}{x^2} \right)$

Comparing coefficients of terms within the parentheses:

1. Constant term: $l = 1$.
2. Coefficient of $\frac{\ln x}{x}$: $m = -1$.
3. Coefficient of $\frac{1}{x}$: $n = -1$.
4. Coefficient of $\frac{\ln x}{x^2}$: $-m = 1 \implies m = -1$. (Consistent with point 2)
5. Coefficient of $\frac{1}{x^2}$: $m-n = 0$. Using $m=-1, n=-1$, we get $(-1) - (-1) = 0$. (Consistent)

So, we found $l=1, m=-1, n=-1$. The problem states that $l,m,n \in N$, which means they must be natural numbers (positive integers). Our values $m=-1$ and $n=-1$ contradict this condition.

However, in competitive exams, when such a contradiction arises, it usually implies that the problem setter intended for $l,m,n$ to be integers.

If the question is exactly as written and $l,m,n$ must be natural numbers, then this problem has no solution as stated.

Assuming the integral is correctly solved to $e^x \left( \frac{x - \ln x - 1}{x} \right)$, then $l=1, m=-1, n=-1$.

Let's proceed with these values assuming the "natural numbers" constraint might be a slight misstatement, and "integers" was intended.

$l=1$, $m=-1$, $n=-1$. Then $l-m-n = 1 - (-1) - (-1) = 1 + 1 + 1 = 3$.