Question
Question: If $\int \frac{e^x}{e^{2x}+6e^x+5}dx = -\frac{1}{4} \log_e (\frac{e^x+a}{e^x+b})+c$, then $\frac{|a-...
If ∫e2x+6ex+5exdx=−41loge(ex+bex+a)+c, then 4∣a−b∣ is ...
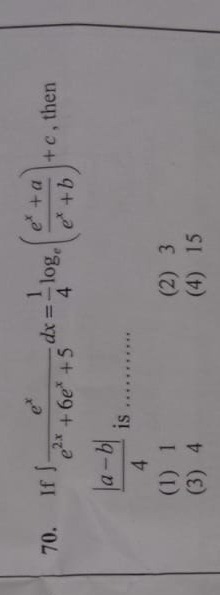
1
3
4
15
1
Solution
To solve the integral ∫e2x+6ex+5exdx, we use a substitution.
Let t=ex. Then, dt=exdx.
Substitute these into the integral: ∫e2x+6ex+5exdx=∫t2+6t+5dt
Now, factor the quadratic in the denominator: t2+6t+5=(t+1)(t+5)
So the integral becomes: ∫(t+1)(t+5)dt
We use partial fraction decomposition for the integrand (t+1)(t+5)1. Let (t+1)(t+5)1=t+1A+t+5B Multiply both sides by (t+1)(t+5): 1=A(t+5)+B(t+1)
To find A, set t=−1: 1=A(−1+5)+B(−1+1) 1=4A⟹A=41
To find B, set t=−5: 1=A(−5+5)+B(−5+1) 1=−4B⟹B=−41
Substitute the values of A and B back into the partial fraction form: (t+1)(t+5)1=t+11/4−t+51/4
Now, integrate: ∫(t+11/4−t+51/4)dt=41∫(t+11−t+51)dt =41(loge∣t+1∣−loge∣t+5∣)+c Using the logarithm property logX−logY=log(X/Y): =41loget+5t+1+c
Substitute back t=ex. Since ex>0, ex+1 and ex+5 are always positive, so we can remove the absolute value signs: ∫e2x+6ex+5exdx=41loge(ex+5ex+1)+c
The problem states that the integral is equal to −41loge(ex+bex+a)+c. We need to equate our result with the given form: 41loge(ex+5ex+1)=−41loge(ex+bex+a) Multiply both sides by 4: loge(ex+5ex+1)=−loge(ex+bex+a) Using the logarithm property −logX=log(1/X): loge(ex+5ex+1)=loge((ex+bex+a)−1) loge(ex+5ex+1)=loge(ex+aex+b) Comparing the arguments of the logarithm: ex+5ex+1=ex+aex+b By comparing the numerators and denominators, we find: b=1 a=5
Finally, we need to calculate 4∣a−b∣: 4∣a−b∣=4∣5−1∣=4∣4∣=44=1
The final answer is 1.
