Question
Question: Which of the following expressions give(s) unit magnitude?...
Which of the following expressions give(s) unit magnitude?
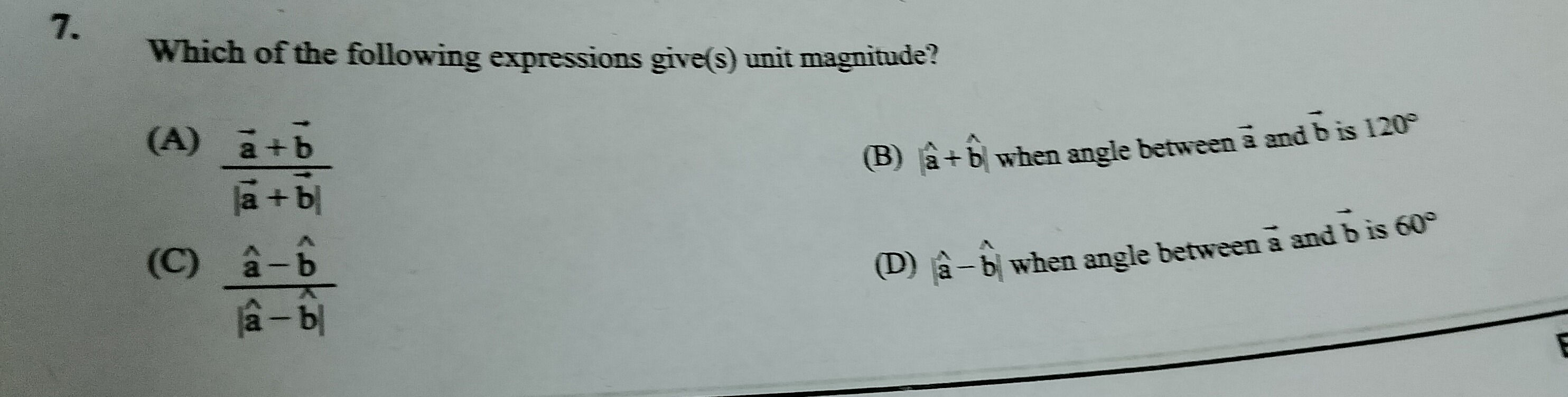
∣a+b∣a+b
∣a^+b^∣ when angle between a and b is 120∘
∣a^−b^∣a^−b^
∣a^−b^∣ when angle between a and b is 60∘
(A), (B), (C), (D)
Solution
Let's analyze each option:
(A) ∣a+b∣a+b
This expression represents a vector. Let v=a+b. The expression is ∣v∣v. This is the definition of a unit vector in the direction of v, provided v=0. The magnitude of a unit vector is always 1. So, if a+b=0, the magnitude of this expression is 1. If a+b=0, the expression is undefined. Assuming the expression is well-defined, it gives a unit magnitude.
(B) ∣a^+b^∣ when angle between a and b is 120∘.
Here, a^ and b^ are unit vectors, so ∣a^∣=1 and ∣b^∣=1. The angle between a^ and b^ is given as θ=120∘.
The magnitude of the sum of two vectors is given by ∣u+v∣=∣u∣2+∣v∣2+2∣u∣∣v∣cosθ.
∣a^+b^∣=∣a^∣2+∣b^∣2+2∣a^∣∣b^∣cos(120∘)
∣a^+b^∣=12+12+2(1)(1)cos(120∘)
∣a^+b^∣=1+1+2(−21)
∣a^+b^∣=2−1=1=1.
The expression gives the scalar value 1, whose magnitude is 1.
(C) ∣a^−b^∣a^−b^
This expression represents a vector. Let w=a^−b^. The expression is ∣w∣w. This is the definition of a unit vector in the direction of w, provided w=0. The magnitude of a unit vector is always 1. So, if a^−b^=0 (i.e., a^=b^), the magnitude of this expression is 1. If a^=b^, the expression is undefined. Assuming the expression is well-defined, it gives a unit magnitude.
(D) ∣a^−b^∣ when angle between a and b is 60∘.
Here, a^ and b^ are unit vectors, so ∣a^∣=1 and ∣b^∣=1. The angle between a^ and b^ is given as θ=60∘.
The magnitude of the difference of two vectors is given by ∣u−v∣=∣u∣2+∣v∣2−2∣u∣∣v∣cosθ.
∣a^−b^∣=∣a^∣2+∣b^∣2−2∣a^∣∣b^∣cos(60∘)
∣a^−b^∣=12+12−2(1)(1)cos(60∘)
∣a^−b^∣=1+1−2(21)
∣a^−b^∣=2−1=1=1.
The expression gives the scalar value 1, whose magnitude is 1.
All four expressions, when well-defined or under the given conditions, result in a quantity with a magnitude of 1. The question asks which expressions give unit magnitude, implying potentially multiple correct options.
