Question

Variable pairs of chords at right angles and drawn through any point P (with eccentric angle $\pi/4$) on the ellipse $\frac{x^2}{4} + y^2 = 1$. to meet the ellipse two points say A and B. If the line joining A and B passes through a fixed point Q(a, b) such that $a^2 + b^2$ has the value equal to $\frac{m}{n}$, where m, n are relatively prime positive integers, find (n - m).

Answer 1

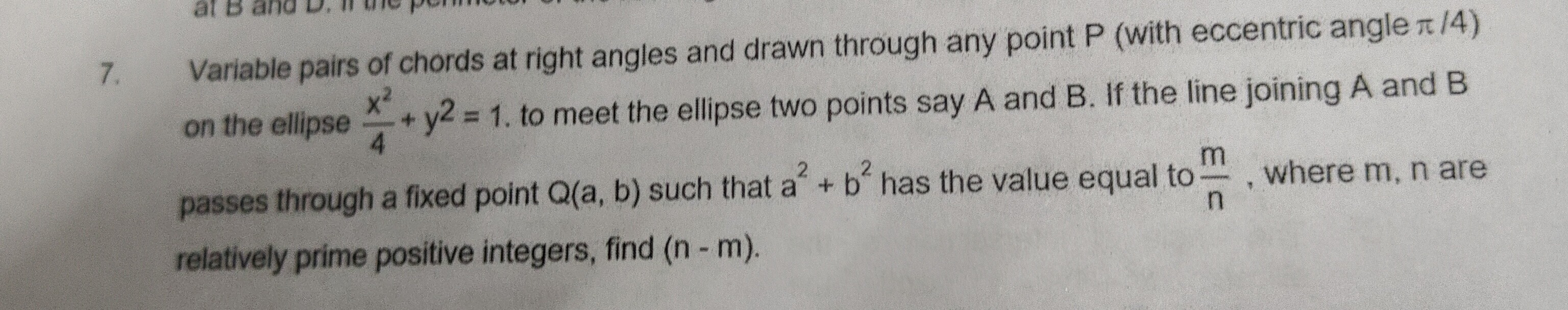
9

Answer 2

The ellipse is given by $\frac{x^2}{4} + y^2 = 1$. The point P on the ellipse with eccentric angle $\pi/4$ has coordinates $(2\cos(\pi/4), 1\sin(\pi/4)) = (\sqrt{2}, 1/\sqrt{2})$.

The equation of the chord of contact of tangents from a point $(x_0, y_0)$ to the ellipse $\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1$ is $\frac{xx_0}{b^2} + \frac{yy_0}{a^2} = 1$. For the given ellipse $\frac{x^2}{4} + y^2 = 1$, we have $a^2=4$ and $b^2=1$. The equation of the chord AB, which is the chord of contact of tangents from P to the ellipse $\frac{x^2}{1^2} + \frac{y^2}{2^2} = 1$ (which is $x^2 + \frac{y^2}{4} = 1$), is: $\frac{x(\sqrt{2})}{1^2} + \frac{y(1/\sqrt{2})}{2^2} = 1$ $\sqrt{2}x + \frac{y}{2\sqrt{2}} = 1$ Multiplying by $2\sqrt{2}$ to clear the denominators: $4x + y = 2\sqrt{2}$ This line AB passes through the fixed point $Q(a, b)$. Thus, the coordinates of Q satisfy the equation of the line: $4a + b = 2\sqrt{2}$ We are given that $a^2 + b^2 = \frac{m}{n}$. To find the value of $a^2+b^2$, we need to find the minimum value of $a^2+b^2$ subject to the constraint $4a+b=2\sqrt{2}$. This minimum occurs at the point Q which is the foot of the perpendicular from the origin to the line $4x+y-2\sqrt{2}=0$.

The distance from the origin $(0,0)$ to the line $4x+y-2\sqrt{2}=0$ is $d = \frac{|4(0) + 1(0) - 2\sqrt{2}|}{\sqrt{4^2 + 1^2}} = \frac{2\sqrt{2}}{\sqrt{17}}$. The square of this distance is $a^2+b^2 = \left(\frac{2\sqrt{2}}{\sqrt{17}}\right)^2 = \frac{8}{17}$.

Alternatively, we can find the coordinates of Q. The line passing through the origin and perpendicular to $4x+y=2\sqrt{2}$ has a slope of $1/4$. Its equation is $y = \frac{1}{4}x$. Substituting this into $4x+y=2\sqrt{2}$: $4x + \frac{1}{4}x = 2\sqrt{2} \implies \frac{17}{4}x = 2\sqrt{2} \implies x = \frac{8\sqrt{2}}{17}$. So $a = \frac{8\sqrt{2}}{17}$. Then $y = \frac{1}{4} \left(\frac{8\sqrt{2}}{17}\right) = \frac{2\sqrt{2}}{17}$. So $b = \frac{2\sqrt{2}}{17}$. $a^2 + b^2 = \left(\frac{8\sqrt{2}}{17}\right)^2 + \left(\frac{2\sqrt{2}}{17}\right)^2 = \frac{128}{289} + \frac{8}{289} = \frac{136}{289} = \frac{8 \times 17}{17 \times 17} = \frac{8}{17}$.

We are given $a^2 + b^2 = \frac{m}{n}$. Thus, $m=8$ and $n=17$. m and n are relatively prime positive integers. We need to find $n-m = 17-8 = 9$.