Question

Two identical spheres each of mass 1.20 kg and radius 10.0 cm are fixed at the ends of a light rod that the separation between the centres is 50.0 cm. Find the moment of inertia of the system about an axis perpendicular to the rod passing through its middle point.

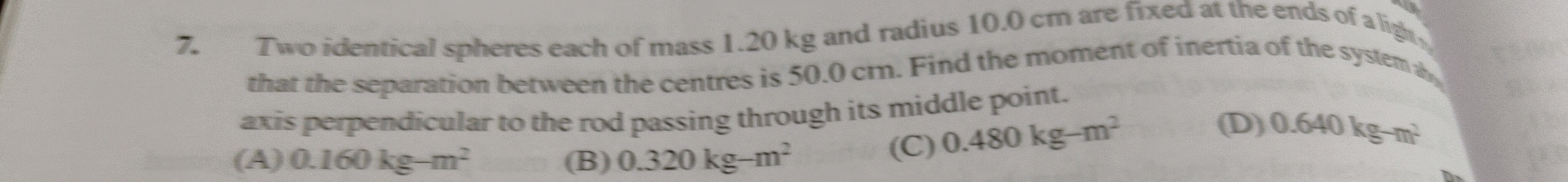
• A. 0.160 kg-m²
• B. 0.320 kg-m²
• C. 0.480 kg-m²
• D. 0.640 kg-m²

Answer 1

Answer: (A)

0.160 kg-m²

Answer 2

The system consists of two identical solid spheres fixed at the ends of a light rod. The axis of rotation is perpendicular to the rod and passes through its midpoint.

1. Given Parameters:

• Mass of each sphere, $m = 1.20$ kg
• Radius of each sphere, $r = 10.0$ cm = $0.10$ m
• Separation between the centers of the spheres, $L = 50.0$ cm = $0.50$ m
• The rod is light, so its moment of inertia is negligible.

2. Moment of Inertia of a single sphere about its own diameter: For a solid sphere, the moment of inertia about an axis passing through its center (diameter) is given by: $I_{cm} = \frac{2}{5}mr^2$

3. Distance of the center of mass of each sphere from the axis of rotation: The axis passes through the midpoint of the rod. Since the total separation between the centers of the spheres is $L$, the distance of the center of each sphere from the axis of rotation is: $d = \frac{L}{2} = \frac{50.0 \text{ cm}}{2} = 25.0 \text{ cm} = 0.25$ m

4. Moment of Inertia of one sphere about the given axis (using Parallel Axis Theorem): According to the parallel axis theorem, the moment of inertia of a sphere about an axis parallel to its diameter and at a distance $d$ from its center is: $I_{sphere} = I_{cm} + md^2$ Substitute the values: $I_{sphere} = \frac{2}{5}mr^2 + md^2$ $I_{sphere} = \frac{2}{5}(1.20 \text{ kg})(0.10 \text{ m})^2 + (1.20 \text{ kg})(0.25 \text{ m})^2$ $I_{sphere} = \frac{2}{5}(1.20)(0.01) + (1.20)(0.0625)$ $I_{sphere} = 0.4 \times 1.20 \times 0.01 + 1.20 \times 0.0625$ $I_{sphere} = 0.0048 + 0.075$ $I_{sphere} = 0.0798 \text{ kg-m}^2$

5. Total Moment of Inertia of the system: Since there are two identical spheres and the system is symmetric about the axis, the total moment of inertia of the system is twice the moment of inertia of one sphere: $I_{total} = 2 \times I_{sphere}$ $I_{total} = 2 \times 0.0798 \text{ kg-m}^2$ $I_{total} = 0.1596 \text{ kg-m}^2$

Rounding to three significant figures, $I_{total} \approx 0.160 \text{ kg-m}^2$.

The final answer is 0.160 kg-m².

Explanation of the solution: The moment of inertia of the system is the sum of the moments of inertia of the two spheres. For each sphere, the moment of inertia about the given axis is calculated using the parallel axis theorem: $I_{sphere} = I_{cm} + md^2$, where $I_{cm} = \frac{2}{5}mr^2$ is the moment of inertia about its own center (diameter), $m$ is the mass, and $d$ is the distance from the sphere's center to the axis of rotation ($d = L/2$). $I_{total} = 2 \times \left( \frac{2}{5}mr^2 + m\left(\frac{L}{2}\right)^2 \right)$ Substitute $m=1.20$ kg, $r=0.10$ m, $L=0.50$ m: $I_{total} = 2 \times \left( \frac{2}{5}(1.20)(0.10)^2 + (1.20)(0.25)^2 \right)$ $I_{total} = 2 \times \left( 0.0048 + 0.075 \right) = 2 \times 0.0798 = 0.1596 \approx 0.160 \text{ kg-m}^2$.