Question
Question: The largest possible set of real numbers which can be the domain of $f(x) = \sqrt{1-\frac{1}{x}}$ is...
The largest possible set of real numbers which can be the domain of f(x)=1−x1 is
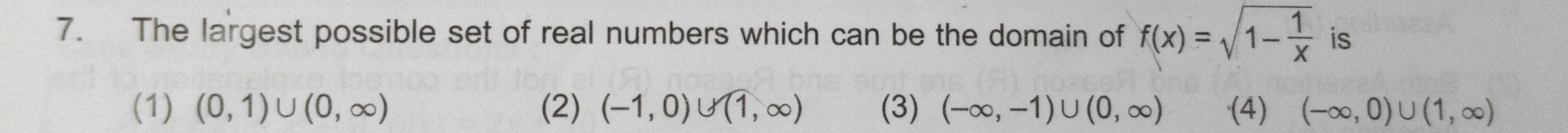
(0, 1) ∪ (0, ∞)
(-1, 0) ∪ (1, ∞)
(-∞, -1) ∪ (0, ∞)
(-∞, 0) ∪ (1, ∞)
(-∞, 0) ∪ (1, ∞)
Solution
To find the domain of the function f(x)=1−x1, we need to ensure that the expression under the square root is non-negative and the denominator of any fraction is not zero.
We require 1−x1≥0, which simplifies to xx−1≥0.
The critical points are x=0 and x=1. We analyze the intervals determined by these points:
-
Interval (−∞,0): Choose x=−1. Then −1−1−1=2≥0. This interval is part of the domain.
-
Interval (0,1): Choose x=0.5. Then 0.50.5−1=−1<0. This interval is not part of the domain.
-
Interval (1,∞): Choose x=2. Then 22−1=21≥0. This interval is part of the domain.
We also need to consider the critical points themselves:
-
x=0 is excluded because it makes the denominator zero in the original function.
-
x=1 is included because f(1)=1−11=0=0, which is a real number.
Therefore, the domain of f(x) is (−∞,0)∪[1,∞).
Among the given options, (−∞,0)∪(1,∞) is the closest, although it incorrectly excludes x=1.
