Question
Question: The differential equation whose solution is $(x - h)^2 + (y - k)^2 = a^2$ (a is given constant) is :...
The differential equation whose solution is (x−h)2+(y−k)2=a2 (a is given constant) is :
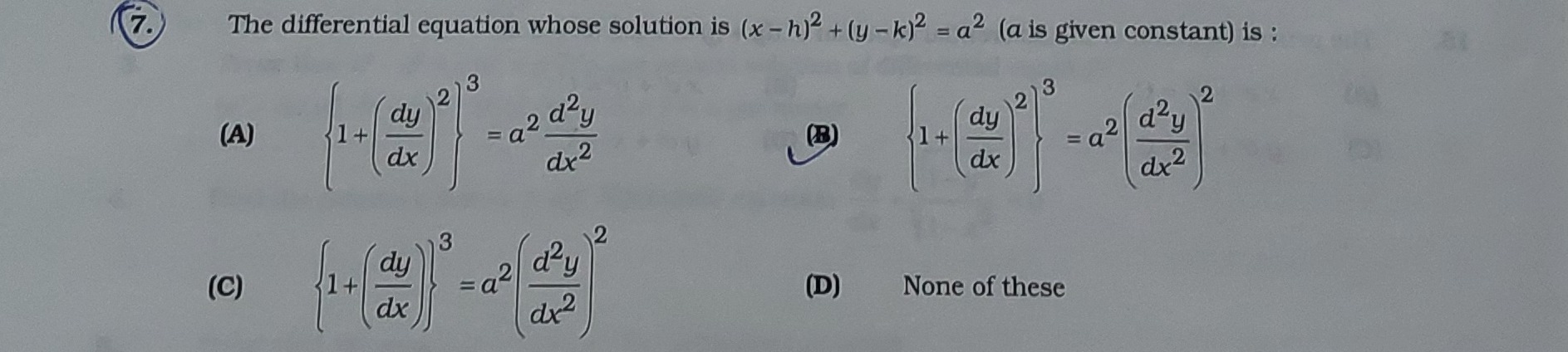
{1+(dxdy)2}3=a2dx2d2y
{1+(dxdy)2}3=a2(dx2d2y)2
{1+(dxdy)2}3=a2(dx2d2y)2
None of these
{1+(dxdy)2}3=a2(dx2d2y)2
Solution
The given equation of the family of curves is:
(x−h)2+(y−k)2=a2…(1)
Here, h and k are arbitrary constants, and a is a given constant. Since there are two arbitrary constants (h and k), we need to differentiate the equation twice to eliminate them.
Step 1: Differentiate equation (1) with respect to x.
Applying the chain rule:
2(x−h)⋅dxd(x−h)+2(y−k)⋅dxd(y−k)=dxd(a2)
2(x−h)(1)+2(y−k)(dxdy)=0
Divide by 2:
(x−h)+(y−k)y′=0…(2)
(where y′=dxdy)
Step 2: Differentiate equation (2) with respect to x.
Applying the product rule for the second term:
dxd(x−h)+dxd((y−k)y′)=dxd(0)
1+((y−k)dxd(y′)+y′dxd(y−k))=0
1+(y−k)y′′+y′(y′)=0
1+(y−k)y′′+(y′)2=0…(3)
(where y′′=dx2d2y)
Step 3: Express (y−k) and (x−h) in terms of y′ and y′′.
From equation (3), we can isolate (y−k):
(y−k)y′′=−(1+(y′)2)
(y−k)=−y′′1+(y′)2…(4)
Now substitute this expression for (y−k) into equation (2) to find (x−h):
(x−h)+(−y′′1+(y′)2)y′=0
(x−h)=y′′y′(1+(y′)2)…(5)
Step 4: Substitute the expressions for (x−h) and (y−k) back into the original equation (1).
Substitute (4) and (5) into (1):
(y′′y′(1+(y′)2))2+(−y′′1+(y′)2)2=a2
(y′′)2(y′)2(1+(y′)2)2+(y′′)2(1+(y′)2)2=a2
Since the denominators are the same, combine the numerators:
(y′′)2(y′)2(1+(y′)2)2+(1+(y′)2)2=a2
Factor out (1+(y′)2)2 from the numerator:
(y′′)2(1+(y′)2)2((y′)2+1)=a2
(y′′)2(1+(y′)2)3=a2
Step 5: Rearrange the equation to match the options.
(1+(y′)2)3=a2(y′′)2
Substitute back y′=dxdy and y′′=dx2d2y:
{1+(dxdy)2}3=a2(dx2d2y)2
This matches option (B). Note that option (C) is identical to option (B), which might be a typo in the question.
