Question
Question: Suppose $f(n)=log_2(3).log_3(4).log_4(5)....log_{n-1}(n)$ then the sum $\sum_{k=2}^{100} f(2^k)$ equ...
Suppose f(n)=log2(3).log3(4).log4(5)....logn−1(n) then the sum ∑k=2100f(2k) equals
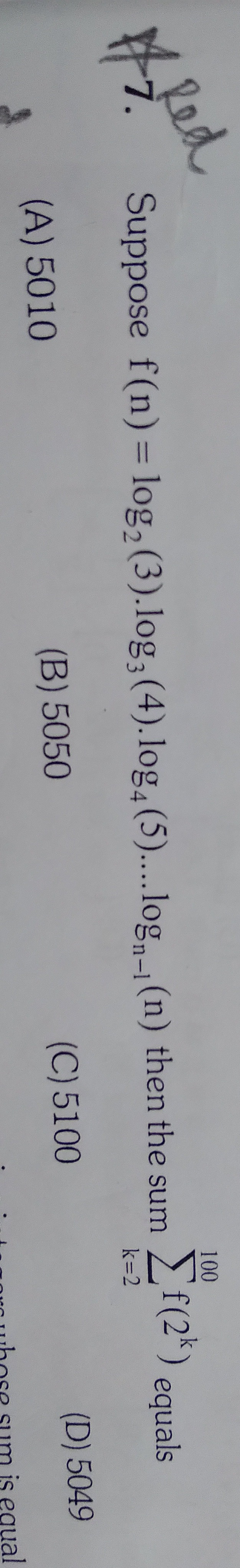
5010
5050
5100
5049
5049
Solution
The function f(n) can be simplified using the change of base formula for logarithms: f(n)=log2(3)⋅log3(4)⋅log4(5)⋯logn−1(n) Using loga(b)=ln(a)ln(b), we get: f(n)=ln(2)ln(3)⋅ln(3)ln(4)⋅ln(4)ln(5)⋯ln(n−1)ln(n) This is a telescoping product, which simplifies to: f(n)=ln(2)ln(n)=log2(n)
Now we need to compute the sum ∑k=2100f(2k): ∑k=2100f(2k)=∑k=2100log2(2k) Using the property loga(ax)=x: ∑k=2100log2(2k)=∑k=2100k
This is the sum of an arithmetic series 2+3+⋯+100. The sum can be calculated as: ∑k=2100k=(∑k=1100k)−1 The sum of the first 100 integers is 2100(100+1)=2100×101=5050. Therefore, the required sum is 5050−1=5049.
