Question
Question: $\lim_{x \to \pi/2} \frac{sin (\pi \csc^2 x)}{(\pi-2x)^2}$...
limx→π/2(π−2x)2sin(πcsc2x)
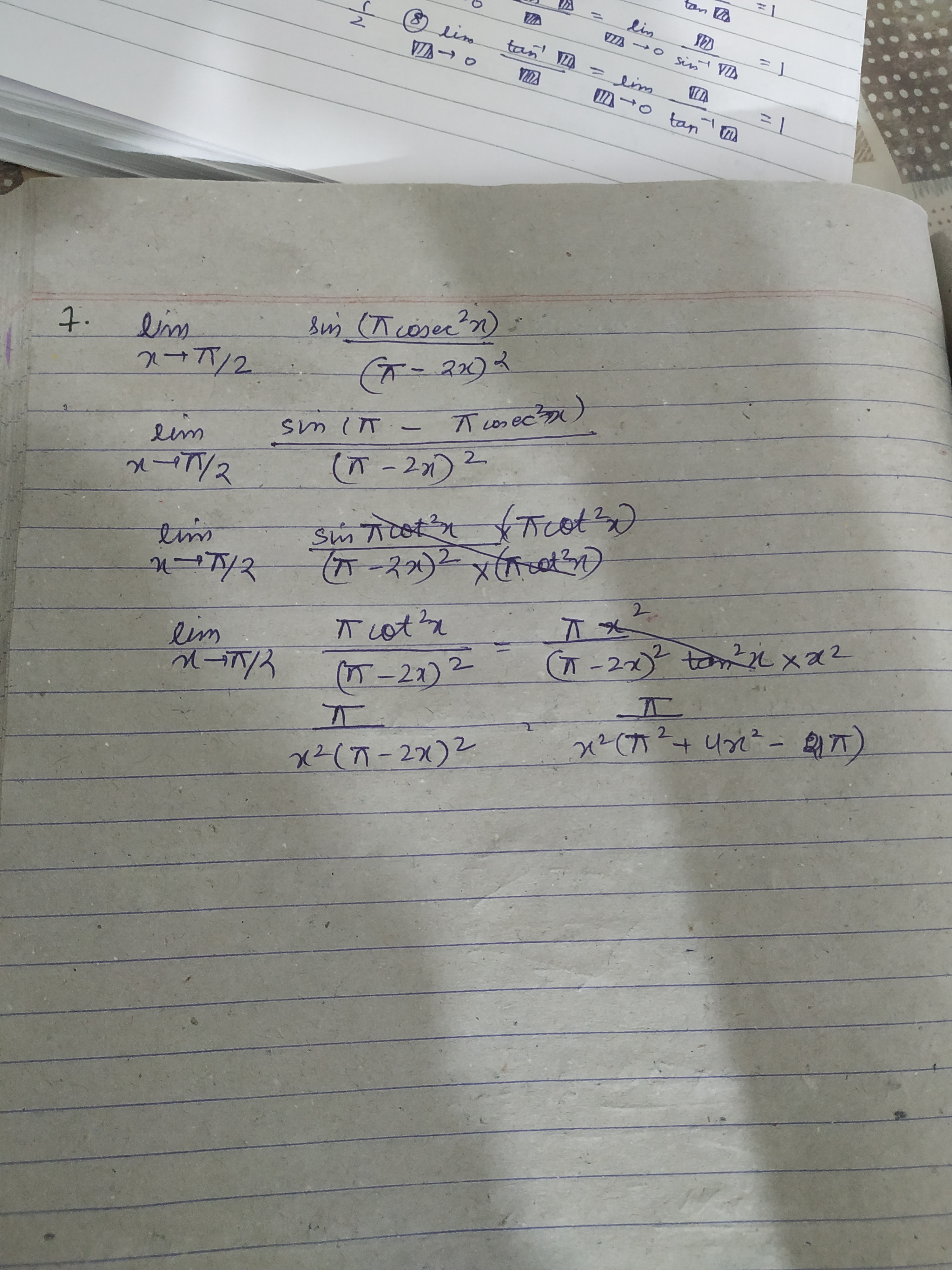
−4π
Solution
To evaluate the limit limx→π/2(π−2x)2sin(πcsc2x):
1. Identify Indeterminate Form:
As x→π/2:
Numerator: sin(πcsc2x)→sin(π⋅12)=sin(π)=0.
Denominator: (π−2x)2→(π−2(π/2))2=(π−π)2=02=0.
The limit is of the indeterminate form 0/0.
2. Transform the Numerator using Trigonometric Identities:
We use the identity sinA=sin(π−A).
So, sin(πcsc2x)=sin(π−πcsc2x).
Factor out π from the argument: π(1−csc2x).
Recall the identity 1+cot2x=csc2x, which implies 1−csc2x=−cot2x.
Substitute this into the argument: π(−cot2x)=−πcot2x.
Therefore, the numerator becomes sin(−πcot2x).
Since sin(−A)=−sinA, we have sin(−πcot2x)=−sin(πcot2x).
The limit expression now is:
limx→π/2(π−2x)2−sin(πcot2x)
3. Apply Standard Limit limy→0ysiny=1:
As x→π/2, cotx→cot(π/2)=0. So, πcot2x→0.
Let y=πcot2x. We can multiply and divide by y to use the standard limit:
limx→π/2(−πcot2xsin(πcot2x)⋅(π−2x)2πcot2x)
The first part, limx→π/2πcot2x−sin(πcot2x), evaluates to −1 as y→0.
So, the limit simplifies to:
−1⋅limx→π/2(π−2x)2πcot2x
4. Simplify and Use Substitution:
Rewrite cot2x as sin2xcos2x:
−πlimx→π/2(π−2x)2sin2xcos2x
As x→π/2, sin2x→sin2(π/2)=12=1.
So, the expression becomes:
−πlimx→π/2(π−2x)2cos2x
Let x=π/2−h. As x→π/2, h→0.
Substitute x=π/2−h:
- cosx=cos(π/2−h)=sinh
- π−2x=π−2(π/2−h)=π−π+2h=2h
Substitute these into the limit expression:
−πlimh→0(2h)2(sinh)2
−πlimh→04h2sin2h
−πlimh→041(hsinh)2
Using the standard limit limh→0hsinh=1:
−π⋅41(1)2=−4π
The final answer is −4π.
Explanation of the solution:
The limit is of the form 0/0. Transform the numerator sin(πcsc2x) to −sin(πcot2x) using sinA=sin(π−A) and 1−csc2x=−cot2x. Apply the standard limit limy→0ysiny=1. The problem reduces to evaluating limx→π/2(π−2x)2−πcot2x. Convert cot2x to sin2xcos2x. Substitute x=π/2−h and simplify using cos(π/2−h)=sinh and π−2x=2h. The limit becomes −πlimh→04h2sin2h, which evaluates to −π/4.
