Question

Let $f$ be a function given by

$$f(x) = \begin{cases} \dfrac{1}{\dfrac{1}{x\ln2}-2^{x}-1}, & x \neq 0,\\[6pt] \dfrac{1}{2}, & x = 0. \end{cases}$$

Then:

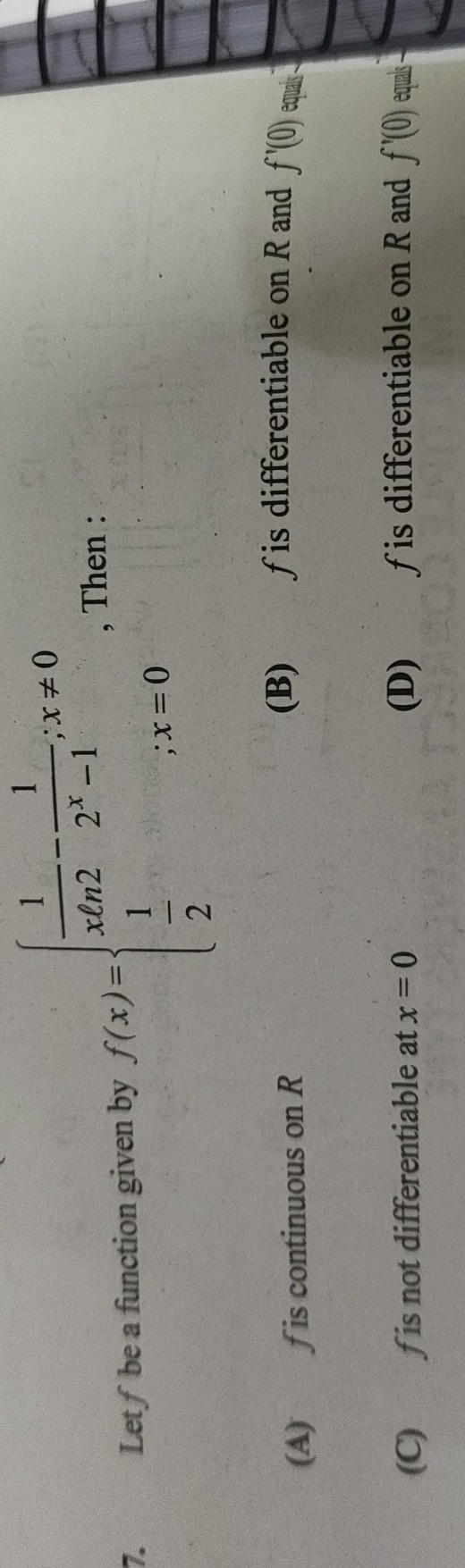
• A. $f$ is continuous on $\mathbb{R}$
• B. $f$ is differentiable on $\mathbb{R}$ and $f'(0)$ equals $\displaystyle -\tfrac{(\ln2)^2}{4}$
• C. $f$ is not differentiable at $x = 0$
• D. $f$ is differentiable on $\mathbb{R}$ and $f'(0)$ equals $\displaystyle \tfrac{(\ln2)^2}{4}$

Answer 1

Answer: (C)

$f$ is not differentiable at $x = 0$

Answer 2

Limit as $x\to0$
Denominator:

$$\frac1{x\ln2}-2^x-1 =\frac1{x\ln2}-\bigl(1+x\ln2+\tfrac{(x\ln2)^2}{2}+\cdots\bigr)-1 \approx \frac1{x\ln2}-2 -x\ln2 -\cdots.$$

Hence

$$f(x) =\frac{1}{\frac1{x\ln2}-2^x-1} \sim \frac{x\ln2}{\,1 - (2+x\ln2+\cdots)\,x\ln2\,} \to 0\quad(\text{as }x\to0).$$

But $f(0)=\tfrac12$.

Conclusion:
• $\lim_{x\to0}f(x)=0\neq f(0)$, so $f$ is discontinuous at 0.
• Hence $f$ cannot be differentiable at $x=0$.