Question

$\int \frac{5(x^6+1)}{x^2+1}dx =$

(where C is a constant of integration.)

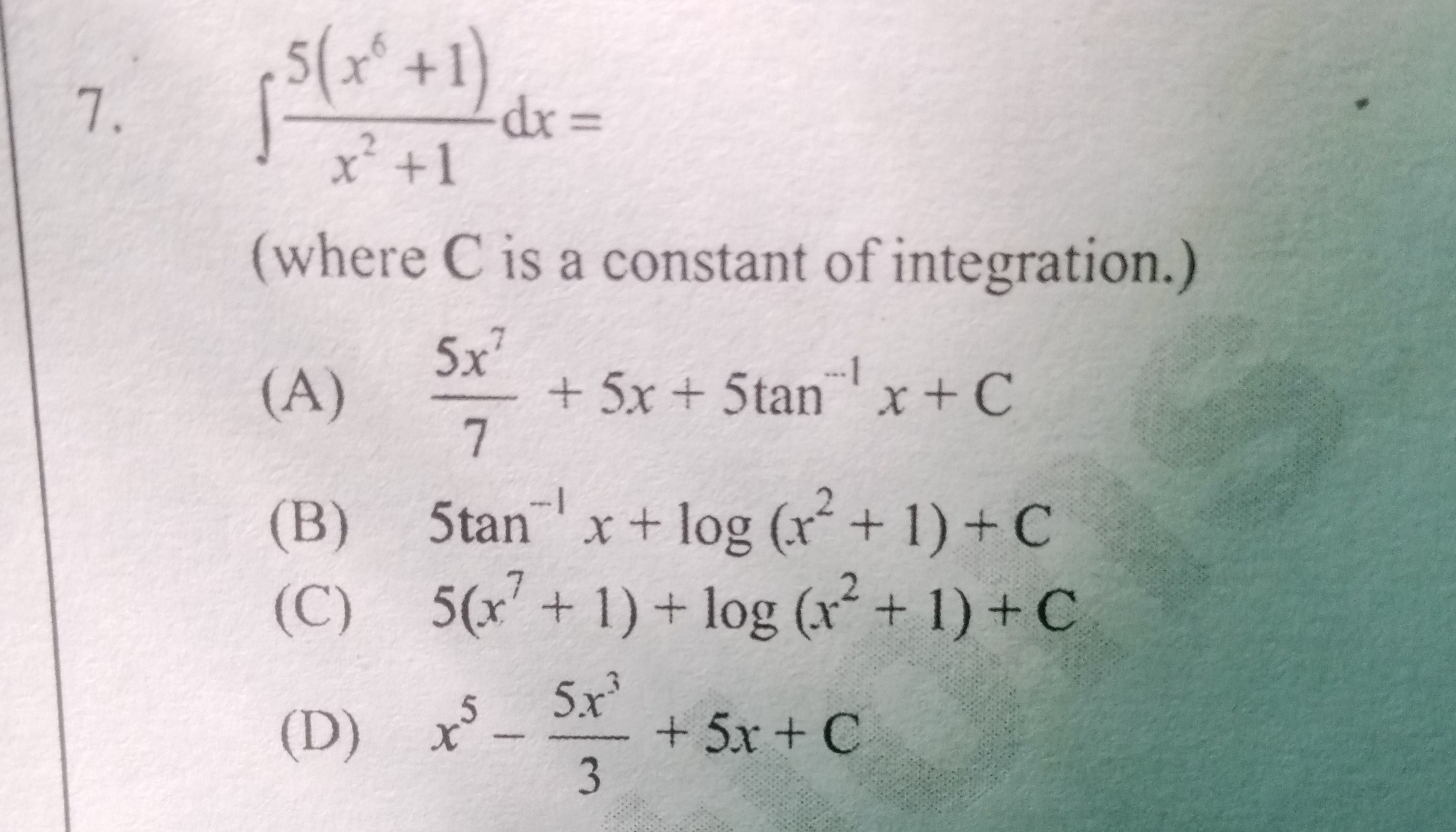
• A. $\frac{5x^7}{7} + 5x + 5\tan^{-1}x + C$
• B. $5\tan^{-1}x + \log(x^2+1) + C$
• C. $5(x^7+1) + \log(x^2+1) + C$
• D. $x^5 - \frac{5x^3}{3} + 5x + C$

Answer 1

Answer: (D)

$x^5 - \frac{5x^3}{3} + 5x + C$

Answer 2

To solve the integral $\int \frac{5(x^6+1)}{x^2+1}dx$, we first simplify the integrand $\frac{x^6+1}{x^2+1}$.

We can use algebraic factorization for the numerator $x^6+1$. This is a sum of cubes, where $x^6 = (x^2)^3$ and $1 = 1^3$. Using the formula $a^3+b^3 = (a+b)(a^2-ab+b^2)$, we let $a=x^2$ and $b=1$: $x^6+1 = (x^2)^3 + 1^3 = (x^2+1)((x^2)^2 - x^2 \cdot 1 + 1^2) = (x^2+1)(x^4-x^2+1)$.

Now substitute this back into the integrand: $\frac{x^6+1}{x^2+1} = \frac{(x^2+1)(x^4-x^2+1)}{x^2+1}$. Since $x^2+1$ is never zero for real $x$, we can cancel the term $(x^2+1)$: $\frac{x^6+1}{x^2+1} = x^4-x^2+1$.

The integral becomes: $\int \frac{5(x^6+1)}{x^2+1}dx = \int 5(x^4-x^2+1)dx$. We can take the constant factor 5 out of the integral: $= 5 \int (x^4-x^2+1)dx$

Now, integrate each term using the power rule for integration, $\int x^n dx = \frac{x^{n+1}}{n+1} + C$ (for $n \neq -1$), and the integral of a constant, $\int c dx = cx + C$:

$\int x^4 dx = \frac{x^{4+1}}{4+1} = \frac{x^5}{5}$

$\int -x^2 dx = -\int x^2 dx = -\frac{x^{2+1}}{2+1} = -\frac{x^3}{3}$

$\int 1 dx = x$

So, the integral is: $5 \left( \frac{x^5}{5} - \frac{x^3}{3} + x \right) + C = 5 \cdot \frac{x^5}{5} - 5 \cdot \frac{x^3}{3} + 5 \cdot x + C = x^5 - \frac{5x^3}{3} + 5x + C$