Question
Question: If y = 2x + k touches $(x - 1)^2 + (y + 2)^2 = 1$, then find k and point of contact (given k > -2)....
If y = 2x + k touches (x−1)2+(y+2)2=1, then find k and point of contact (given k > -2).
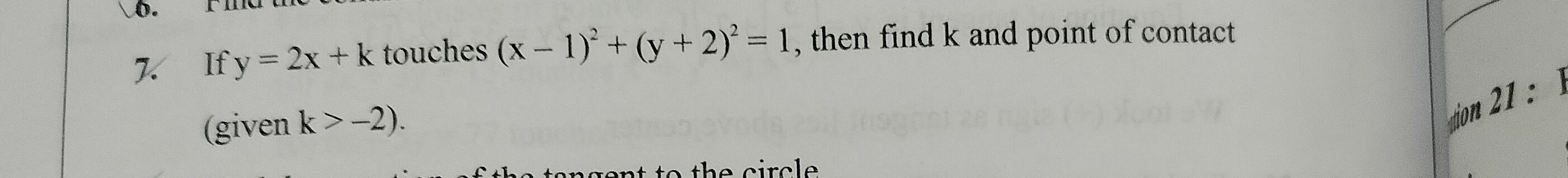
k = 5−4, Point of contact: (1−525,−2+55)
k = −5−4, Point of contact: (1+525,−2−55)
k = 5+4, Point of contact: (1+525,−2+55)
k = −5+4, Point of contact: (1−525,−2−55)
k = 5−4, Point of contact: (1−525,−2+55)
Solution
The circle (x−1)2+(y+2)2=1 has its center at C(1,−2) and radius r=1. The line y=2x+k can be written as 2x−y+k=0. For the line to be tangent to the circle, the perpendicular distance from the center to the line must be equal to the radius. d=22+(−1)2∣2(1)−(−2)+k∣=5∣4+k∣ Setting d=r=1: 5∣4+k∣=1⟹∣4+k∣=5 This gives two possibilities:
- 4+k=5⟹k=5−4
- 4+k=−5⟹k=−5−4
Given the condition k>−2: Since 5≈2.236, k1=5−4≈2.236−4=−1.764, which is greater than −2. k2=−5−4≈−2.236−4=−6.236, which is less than −2. Thus, we choose k=5−4.
The point of contact (x0,y0) is the foot of the perpendicular from the center C(1,−2) to the tangent line 2x−y+(5−4)=0. Using the formula for the foot of the perpendicular: Ax0−x1=By0−y1=−A2+B2Ax1+By1+C 2x0−1=−1y0−(−2)=−22+(−1)22(1)−1(−2)+(5−4) 2x0−1=−1y0+2=−4+12+2+5−4 2x0−1=−1y0+2=−55 Equating the first part with the result: 2x0−1=−55⟹x0−1=−525⟹x0=1−525 Equating the second part with the result: −1y0+2=−55⟹y0+2=55⟹y0=−2+55 The point of contact is (1−525,−2+55).
