Solveeit Logo
Login

Question

Question: If x, y, z are all different real numbers, then prove that $\frac{1}{(x-y)^2}+\frac{1}{(y-z)^2}+\fr...

If x, y, z are all different real numbers, then prove that

1(x−y)2+1(y−z)2+1(z−x)2=(1x−y+1y−z+1z−x)2\frac{1}{(x-y)^2}+\frac{1}{(y-z)^2}+\frac{1}{(z-x)^2}=\left(\frac{1}{x-y}+\frac{1}{y-z}+\frac{1}{z-x}\right)^2.

Solve for x:

Answer

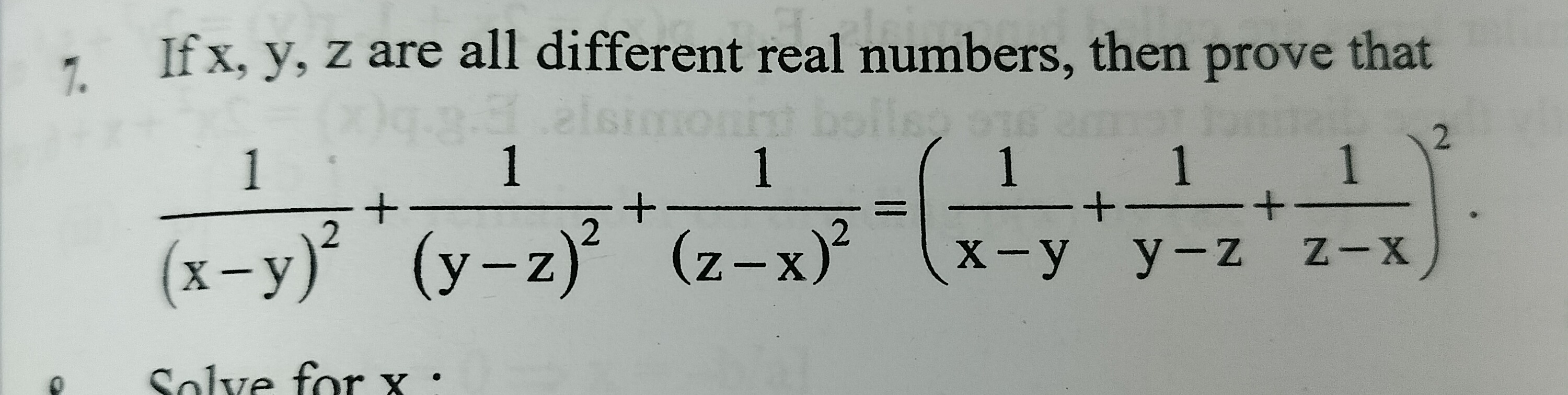
The question is incomplete as the equation to be solved for x is missing. The first part of the question is proven below.

Explanation

Solution

Let A=1x−yA = \frac{1}{x-y}, B=1y−zB = \frac{1}{y-z}, and C=1z−xC = \frac{1}{z-x}. Since x,y,zx, y, z are all different real numbers, x−y≠0x-y \neq 0, y−z≠0y-z \neq 0, and z−x≠0z-x \neq 0. Thus, A,B,CA, B, C are well-defined non-zero real numbers.

The identity to be proven can be written in terms of A,B,CA, B, C as: A2+B2+C2=(A+B+C)2A^2 + B^2 + C^2 = (A+B+C)^2 We know the algebraic identity for the square of a trinomial: (A+B+C)2=A2+B2+C2+2(AB+BC+CA)(A+B+C)^2 = A^2 + B^2 + C^2 + 2(AB+BC+CA) For the identity A2+B2+C2=(A+B+C)2A^2 + B^2 + C^2 = (A+B+C)^2 to hold, it must be true that 2(AB+BC+CA)=02(AB+BC+CA) = 0, which simplifies to AB+BC+CA=0AB+BC+CA = 0.

Let's calculate the sum of the products AB+BC+CAAB+BC+CA using the definitions of A,B,CA, B, C: AB=1x−y⋅1y−z=1(x−y)(y−z)AB = \frac{1}{x-y} \cdot \frac{1}{y-z} = \frac{1}{(x-y)(y-z)} BC=1y−z⋅1z−x=1(y−z)(z−x)BC = \frac{1}{y-z} \cdot \frac{1}{z-x} = \frac{1}{(y-z)(z-x)} CA=1z−x⋅1x−y=1(z−x)(x−y)CA = \frac{1}{z-x} \cdot \frac{1}{x-y} = \frac{1}{(z-x)(x-y)} Now, sum these products: AB+BC+CA=1(x−y)(y−z)+1(y−z)(z−x)+1(z−x)(x−y)AB+BC+CA = \frac{1}{(x-y)(y-z)} + \frac{1}{(y-z)(z-x)} + \frac{1}{(z-x)(x-y)} To add these fractions, we find a common denominator, which is (x−y)(y−z)(z−x)(x-y)(y-z)(z-x). AB+BC+CA=(z−x)(x−y)(y−z)(z−x)+(x−y)(y−z)(z−x)(x−y)+(y−z)(z−x)(x−y)(y−z)AB+BC+CA = \frac{(z-x)}{(x-y)(y-z)(z-x)} + \frac{(x-y)}{(y-z)(z-x)(x-y)} + \frac{(y-z)}{(z-x)(x-y)(y-z)} The sum of the numerators is: (z−x)+(x−y)+(y−z)=z−x+x−y+y−z=0(z-x) + (x-y) + (y-z) = z - x + x - y + y - z = 0 Since x,y,zx, y, z are distinct, the denominator (x−y)(y−z)(z−x)(x-y)(y-z)(z-x) is non-zero. Therefore, the sum of the fractions is: AB+BC+CA=0(x−y)(y−z)(z−x)=0AB+BC+CA = \frac{0}{(x-y)(y-z)(z-x)} = 0 Now substitute this result back into the algebraic identity for (A+B+C)2(A+B+C)^2: (A+B+C)2=A2+B2+C2+2(0)(A+B+C)^2 = A^2 + B^2 + C^2 + 2(0) (A+B+C)2=A2+B2+C2(A+B+C)^2 = A^2 + B^2 + C^2 Substituting back the expressions for A,B,CA, B, C: (1x−y+1y−z+1z−x)2=(1x−y)2+(1y−z)2+(1z−x)2\left(\frac{1}{x-y}+\frac{1}{y-z}+\frac{1}{z-x}\right)^2 = \left(\frac{1}{x-y}\right)^2 + \left(\frac{1}{y-z}\right)^2 + \left(\frac{1}{z-x}\right)^2 (1x−y+1y−z+1z−x)2=1(x−y)2+1(y−z)2+1(z−x)2\left(\frac{1}{x-y}+\frac{1}{y-z}+\frac{1}{z-x}\right)^2 = \frac{1}{(x-y)^2} + \frac{1}{(y-z)^2} + \frac{1}{(z-x)^2} This proves the given identity.