Question
Question: If sin($\alpha + \beta$) = 1, sin($\alpha - \beta$) = $\frac{1}{2}$, then tan($\alpha + 2\beta$)tan(...
If sin(α+β) = 1, sin(α−β) = 21, then tan(α+2β)tan(2α+β) =
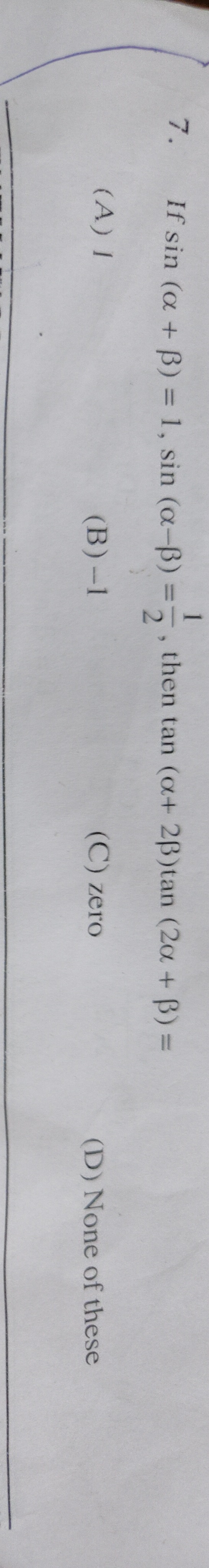
1
-1
zero
None of these
1
Solution
To solve the problem, we first determine the values of (α+β) and (α−β) from the given sine equations.
Given:
- sin(α+β)=1
- sin(α−β)=21
From equation (1), for the principal value, we have: α+β=2π (Equation A)
From equation (2), for the principal value, we have: α−β=6π (Equation B)
Now, we solve the system of linear equations (A) and (B) for α and β.
Add Equation A and Equation B: (α+β)+(α−β)=2π+6π 2α=63π+π 2α=64π 2α=32π α=3π
Substitute the value of α into Equation A: 3π+β=2π β=2π−3π β=63π−2π β=6π
So, we have α=3π and β=6π.
Next, we need to find the values of the arguments for the tangent functions: (α+2β) and (2α+β).
Calculate (α+2β): α+2β=3π+2(6π) =3π+3π =32π
Calculate (2α+β): 2α+β=2(3π)+6π =32π+6π =64π+π =65π
Now, calculate the tangent of these angles: tan(α+2β)=tan(32π) We know that tan(π−x)=−tan(x). tan(32π)=tan(π−3π)=−tan(3π)=−3
tan(2α+β)=tan(65π) We know that tan(π−x)=−tan(x). tan(65π)=tan(π−6π)=−tan(6π)=−31
Finally, multiply the two tangent values: tan(α+2β)tan(2α+β)=(−3)×(−31) =1
