Question

If L = cos² 84° + cos² 36° + cos 36° cos 84° M = cot 73° cot 47° cot 13° N = 4 sin 156° sin 84° sin36°, then which of the following option(s) is(are) correct?

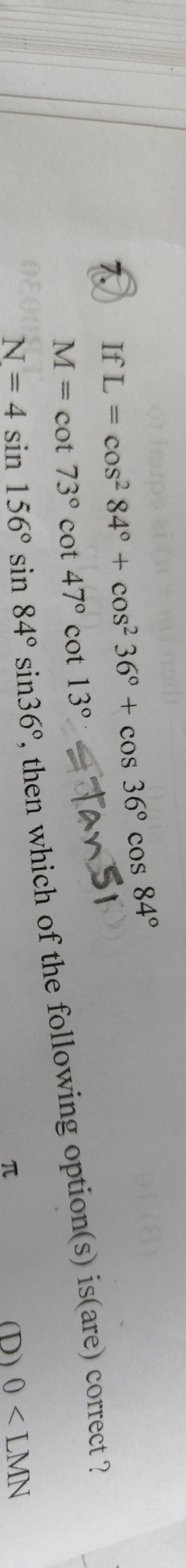
• A. 0 < LMN

Answer 1

Answer: (A)

0 < LMN < π

Answer 2

To solve the problem, we need to evaluate the expressions L, M, and N first, and then check the given option.

1. Evaluating L: L = cos² 84° + cos² 36° + cos 36° cos 84° We use the identity: $\cos^2 A + \cos^2 B = 1 + \cos(A+B)\cos(A-B)$. Let A = 84° and B = 36°. So, $\cos^2 84° + \cos^2 36° = 1 + \cos(84°+36°)\cos(84°-36°)$ $= 1 + \cos(120°)\cos(48°)$ $= 1 + (-\frac{1}{2})\cos(48°)$ $= 1 - \frac{1}{2}\cos(48°)$.

Now, consider the term $\cos 36° \cos 84°$. Using the product-to-sum identity: $2 \cos A \cos B = \cos(A+B) + \cos(A-B)$. $\cos 36° \cos 84° = \frac{1}{2}[\cos(36°+84°) + \cos(36°-84°)]$ $= \frac{1}{2}[\cos(120°) + \cos(-48°)]$ $= \frac{1}{2}[-\frac{1}{2} + \cos(48°)]$ $= -\frac{1}{4} + \frac{1}{2}\cos(48°)$.

Substitute these back into the expression for L: L = $(1 - \frac{1}{2}\cos(48°)) + (-\frac{1}{4} + \frac{1}{2}\cos(48°))$ L = $1 - \frac{1}{4}$ L = $\frac{3}{4}$.

2. Evaluating M: M = cot 73° cot 47° cot 13° We observe the angles: $13°$, $47° = 60° - 13°$, and $73° = 60° + 13°$. This matches the form of the identity: $\cot A \cot(60°-A) \cot(60°+A) = \cot(3A)$. Here, A = 13°. So, M = $\cot(3 \times 13°)$ M = $\cot 39°$.

3. Evaluating N: N = 4 sin 156° sin 84° sin 36° First, use the identity $\sin(180°-x) = \sin x$: $\sin 156° = \sin(180°-24°) = \sin 24°$. So, N = 4 sin 24° sin 84° sin 36°. We observe the angles: $24°$, $36° = 60° - 24°$, and $84° = 60° + 24°$. This matches the form of the identity: $\sin A \sin(60°-A) \sin(60°+A) = \frac{1}{4}\sin(3A)$. Here, A = 24°. So, N = $4 \times \frac{1}{4}\sin(3 \times 24°)$ N = $\sin 72°$.

4. Checking the option 0 < LMN < $\pi$: We have L = 3/4, M = cot 39°, N = sin 72°. LMN = $\frac{3}{4} \cot 39° \sin 72°$.

First, let's check if LMN > 0. Since $0 < 3/4 < 1$, $3/4$ is positive. Since $0° < 39° < 90°$, $\cot 39°$ is positive. Since $0° < 72° < 90°$, $\sin 72°$ is positive. The product of three positive numbers is positive, so LMN > 0 is true.

Next, let's check if LMN < $\pi$. We know that $\pi \approx 3.14159$. We can rewrite LMN as: LMN = $\frac{3}{4} \frac{\cos 39°}{\sin 39°} \sin 72°$. We also know that $\sin 72° = \cos(90°-72°) = \cos 18°$. So, LMN = $\frac{3}{4} \frac{\cos 39°}{\sin 39°} \cos 18°$.

Let's estimate the values: $\cos 18° \approx 0.951$ (since $\cos 18° = \frac{\sqrt{10+2\sqrt{5}}}{4}$) $\sin 39° \approx \sin 45° = \frac{1}{\sqrt{2}} \approx 0.707$ $\cos 39° \approx \cos 45° = \frac{1}{\sqrt{2}} \approx 0.707$ $\cot 39° \approx 1$. More precisely, $\cot 30° = \sqrt{3} \approx 1.732$ and $\cot 45° = 1$. So $\cot 39°$ is between 1 and 1.732.

Let's use a more precise estimate or bound: Since $39° < 45°$, $\cot 39° > \cot 45° = 1$. Since $72° < 90°$, $\sin 72° < \sin 90° = 1$. Since $72° > 60°$, $\sin 72° > \sin 60° = \frac{\sqrt{3}}{2} \approx 0.866$. So, $LMN = \frac{3}{4} \cot 39° \sin 72°$. We know $\cot 39° < \cot 30° = \sqrt{3}$. So, $LMN < \frac{3}{4} \times \sqrt{3} \times 1 = \frac{3\sqrt{3}}{4} \approx \frac{3 \times 1.732}{4} = \frac{5.196}{4} = 1.299$. Since $1.299 < \pi \approx 3.14159$, the condition LMN < $\pi$ holds true.

Therefore, $0 < LMN < \pi$ is correct.

The final answer is $\boxed{0 < LMN < \pi}$.