Question
Question: If $k \in R$, then det$\{adj(kI_n)\}$ is equal to...
If k∈R, then det{adj(kIn)} is equal to
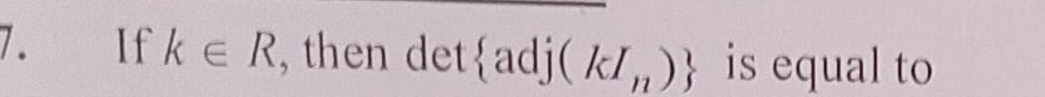
k^{n(n-1)}
Solution
To find det(adj(kIn)), we use the properties of determinants and adjoint matrices.
Let A=kIn. Here, In is the n×n identity matrix, and k∈R is a scalar.
Step 1: Calculate the determinant of A. The matrix A=kIn is a diagonal matrix with k along the main diagonal: A=k0⋮00k⋮0……⋱…00⋮kn×n The determinant of A is given by: det(A)=det(kIn) Using the property that for a scalar c and an n×n matrix M, det(cM)=cndet(M): det(kIn)=kndet(In) Since the determinant of an identity matrix is 1 (det(In)=1): det(A)=kn⋅1=kn
Step 2: Use the property of the determinant of an adjoint matrix. For any n×n matrix M, the determinant of its adjoint is given by the formula: det(adj(M))=(det(M))n−1 This formula is generally valid for invertible matrices (i.e., det(M)=0).
Step 3: Substitute det(A) into the formula. Substitute det(A)=kn into the formula for det(adj(A)): det(adj(kIn))=(det(kIn))n−1=(kn)n−1 Using the exponent rule (ab)c=abc: det(adj(kIn))=kn(n−1)
Step 4: Verify for the special case when k=0. The formula det(adj(M))=(det(M))n−1 is typically derived assuming det(M)=0. Let's check if our result holds when k=0.
If k=0, then A=0⋅In=On (the n×n zero matrix). We need to find det(adj(On)).
-
Case 1: n=1 A=[0]. The adjoint of a 1×1 matrix [a] is defined as [1]. So, adj([0])=[1]. det(adj([0]))=det([1])=1. Our formula kn(n−1) gives 01(1−1)=00. If we adopt the convention 00=1 (which is common in such contexts), the formula holds.
-
Case 2: n>1 A=On. The adjoint matrix adj(On) is the transpose of the cofactor matrix. For n>1, any (n−1)×(n−1) submatrix of On will be a zero matrix of size (n−1)×(n−1). The determinant of such a submatrix is 0. Therefore, all minors Mij are 0, which implies all cofactors Cij=(−1)i+jMij are also 0. Thus, adj(On)=On. det(adj(On))=det(On)=0. Our formula kn(n−1) gives 0n(n−1). Since n>1, n(n−1) is a positive integer (e.g., for n=2, n(n−1)=2; for n=3, n(n−1)=6). Any positive integer power of 0 is 0. So, 0n(n−1)=0. The formula holds for n>1 and k=0.
Since the formula kn(n−1) holds for all k∈R and n∈N (with the standard convention 00=1), it is the general solution.
