Question
Question: If F: R→ R is a differentiable function and f(3) = 6, then $\lim_{x\to3} \int_{6}^{f(x)} \frac{2tdt}...
If F: R→ R is a differentiable function and f(3) = 6, then limx→3∫6f(x)(x−2)2tdt is equal to
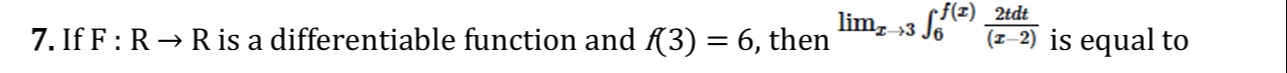
0
Solution
Let the given limit be L. The expression is limx→3∫6f(x)(x−2)2tdt. The term (x−2) in the denominator is constant with respect to the integration variable t. So we can take it out of the integral: L=limx→3x−21∫6f(x)2tdt.
First, let's evaluate the definite integral ∫6f(x)2tdt: ∫2tdt=t2. So, ∫6f(x)2tdt=[t2]6f(x)=(f(x))2−62=(f(x))2−36.
Now, substitute this back into the limit expression: L=limx→3x−2(f(x))2−36.
We need to evaluate this limit. Let's examine the behavior of the numerator and the denominator as x→3. The denominator is x−2. As x→3, the denominator approaches 3−2=1. The numerator is (f(x))2−36. Since f is a differentiable function, it is also continuous. Thus, limx→3f(x)=f(3). We are given that f(3)=6. So, as x→3, the numerator approaches (f(3))2−36=62−36=36−36=0.
The limit is of the form 10. L=limx→3(x−2)limx→3((f(x))2−36)=10=0.
The limit is 0.
