Solveeit Logo
Login

Question

Question: If each of the resistance in the circuit is 20Ω, the equivalent resistance between terminals A and B...

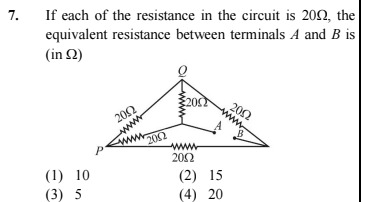
If each of the resistance in the circuit is 20Ω, the equivalent resistance between terminals A and B is (in Ω)

A

10

B

15

C

5

D

20

Answer

40/3

Explanation

Solution

The circuit has 6 resistors, each of resistance R = 20Ω. We need to find the equivalent resistance between terminals A and B. From the diagram, terminal A is the central node (let's call it C) and terminal B is the bottom-right node (let's call it N).

Let's label the nodes as P (top-left), Q (top-right), M (bottom-left), C (center), and N (bottom-right). We apply nodal analysis by setting the potential at C to V and at N to 0. Let V_P, V_Q, and V_M be the potentials at nodes P, Q, and M respectively.

  1. KCL at node P: V−VPR+VQ−VPR=0  ⟹  V+VQ=2VP(1)\frac{V - V_P}{R} + \frac{V_Q - V_P}{R} = 0 \implies V + V_Q = 2V_P \quad \text{(1)}

  2. KCL at node Q: V−VQR+VP−VQR=0  ⟹  V+VP=2VQ(2)\frac{V - V_Q}{R} + \frac{V_P - V_Q}{R} = 0 \implies V + V_P = 2V_Q \quad \text{(2)}

  3. KCL at node M: V−VMR+0−VMR=0  ⟹  V=2VM  ⟹  VM=V2(3)\frac{V - V_M}{R} + \frac{0 - V_M}{R} = 0 \implies V = 2V_M \implies V_M = \frac{V}{2} \quad \text{(3)}

Solving (1) and (2) simultaneously: From (1), VQ=2VP−VV_Q = 2V_P - V. Substitute into (2): V+VP=2(2VP−V)V + V_P = 2(2V_P - V) V+VP=4VP−2VV + V_P = 4V_P - 2V 3V=3VP  ⟹  VP=V3V = 3V_P \implies V_P = V Substitute VP=VV_P = V back into (1): V+VQ=2V  ⟹  VQ=VV + V_Q = 2V \implies V_Q = V

So, the potentials are VP=VQ=VC=VV_P = V_Q = V_C = V. This implies that there is no potential difference across resistors R_PC, R_QC, and R_PQ. Therefore, no current flows through these three resistors. They effectively act as open circuits and can be removed for calculating the equivalent resistance between C and N.

The circuit simplifies to the following connections between C and N:

  • A direct resistor R_CN = 20Ω.
  • A path through node M: R_CM (20Ω) in series with R_MN (20Ω).

The series combination of R_CM and R_MN is Rseries=RCM+RMN=20Ω+20Ω=40ΩR_{series} = R_{CM} + R_{MN} = 20\Omega + 20\Omega = 40\Omega. This series combination is in parallel with the direct resistor R_CN. The equivalent resistance ReqR_{eq} between C and N is: Req=Rseries×RCNRseries+RCNR_{eq} = \frac{R_{series} \times R_{CN}}{R_{series} + R_{CN}} Req=40Ω×20Ω40Ω+20ΩR_{eq} = \frac{40\Omega \times 20\Omega}{40\Omega + 20\Omega} Req=80060ΩR_{eq} = \frac{800}{60} \Omega Req=806Ω=403ΩR_{eq} = \frac{80}{6} \Omega = \frac{40}{3} \Omega

Numerically, Req≈13.33ΩR_{eq} \approx 13.33 \Omega.

The calculated value 40/3 Ω is not among the options. This suggests there might be an error in the question's options.